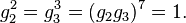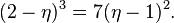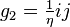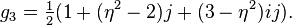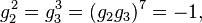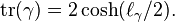(2,3,7) triangle group

In the theory of Riemann surfaces and hyperbolic geometry, the triangle group (2,3,7) is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84(g − 1), of its automorphism group.

A note on terminology – the "(2,3,7) triangle group" most often refers, not to the full triangle group Δ(2,3,7) (the Coxeter group with Schwarz triangle (2,3,7) or a realization as a hyperbolic reflection group), but rather to the ordinary triangle group (the von Dyck group) D(2,3,7) of orientation-preserving maps (the rotation group), which is index 2.

Torsion-free normal subgroups of the (2,3,7) triangle group are Fuchsian groups associated with Hurwitz surfaces, such as the Klein quartic, Macbeath surface and First Hurwitz triplet.

Constructions

Hyperbolic construction

The (2,3,7) triangle group is the group of orientation-preserving isometries of the tiling by the (2,3,7) Schwarz triangle, shown here in a Poincaré disk model projection.

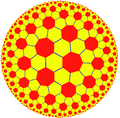
To construct the triangle group, start with a hyperbolic triangle with angles π/2, π/3, π/7. This triangle, the smallest hyperbolic Schwarz triangle, tiles the plane by reflections in its sides. Consider then the group generated by reflections in the sides of the triangle, which (since the triangle tiles) is a non-Euclidean crystallographic group (discrete subgroup of hyperbolic isometries) with this triangle for fundamental domain; the associated tiling is the order-3 bisected heptagonal tiling. The (2,3,7) triangle group is defined as the index 2 subgroup consisting of the orientation-preserving isometries, which is a Fuchsian group (orientation-preserving NEC group).

Uniform heptagonal/triangular tilings
Symmetry: [7,3], (*732)							[7,3]+, (732)
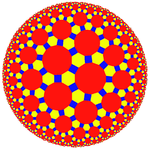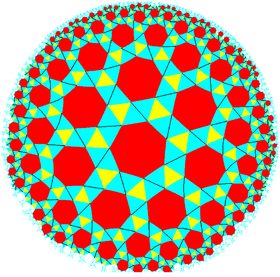{7,3}	t{7,3}	r{7,3}	t{3,7}	{3,7}	rr{7,3}	tr{7,3}	sr{7,3}
Uniform duals
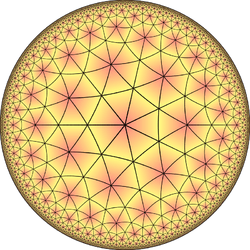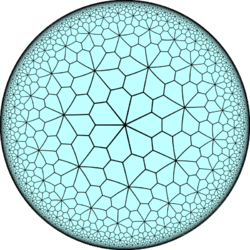V73	V3.14.14	V3.7.3.7	V6.6.7	V37	V3.4.7.4	V4.6.14	V3.3.3.3.7

Group presentation

It has a presentation in terms of a pair of generators, g₂, g₃, modulo the following relations:

Geometrically, these correspond to rotations by 2π/2, 2π/3, 2π/7 about the vertices of the Schwarz triangle.

Quaternion algebra

The (2,3,7) triangle group admits a presentation in terms of the group of quaternions of norm 1 in a suitable order in a quaternion algebra. More specifically, the triangle group is the quotient of the group of quaternions by its center ±1.

Let η = 2cos(2π/7). Then from the identity

we see that Q(η) is a totally real cubic extension of Q. The (2,3,7) hyperbolic triangle group is a subgroup of the group of norm 1 elements in the quaternion algebra generated as an associative algebra by the pair of generators i,j and relations i² = j² = η, ij = −ji. One chooses a suitable Hurwitz quaternion order 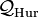in the quaternion algebra. Here the order 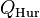is generated by elements

In fact, the order is a free Z[η]-module over the basis 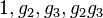. Here the generators satisfy the relations

which descend to the appropriate relations in the triangle group, after quotienting by the center.

Relation to SL(2,R)

Visualization of the map (2,3,∞) → (2,3,7) by morphing the associated tilings.^[1]

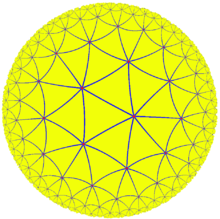
Extending the scalars from Q(η) to R (via the standard imbedding), one obtains an isomorphism between the quaternion algebra and the algebra M(2,R) of real 2 by 2 matrices. Choosing a concrete isomorphism allows one to exhibit the (2,3,7) triangle group as a specific Fuchsian group in SL(2,R), specifically as a quotient of the modular group. This can be visualized by the associated tilings, as depicted at right: the (2,3,7) tiling on the Poincaré disc is a quotient of the modular tiling on the upper half-plane.

However, for many purposes, explicit isomorphisms are unnecessary. Thus, traces of group elements (and hence also translation lengths of hyperbolic elements acting in the upper half-plane, as well as systoles of Fuchsian subgroups) can be calculated by means of the reduced trace in the quaternion algebra, and the formula

References

Further reading