Bipartite half

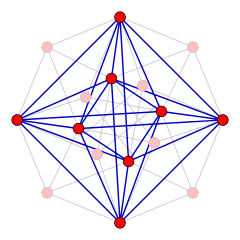
The halved cube graph of order 4, obtained as the bipartite half of an order-4 hypercube graph

In graph theory, the bipartite half or half-square of a bipartite graph G = (U,V,E) is a graph whose vertex set is one of the two sides of the bipartition (without loss of generality, U) and in which there is an edge uiuj for each two vertices ui and uj in U that are at distance two from each other in G.[1] That is, in a more compact notation, the bipartite half is G2[U] where the superscript 2 denotes the square of a graph and the square brackets denote an induced subgraph.

For instance, the bipartite half of the complete bipartite graph Kn,n is the complete graph Kn and the bipartite half of the hypercube graph is the halved cube graph. When G is a distance-regular graph, its two bipartite halves are both distance-regular.[2]

The map graphs, that is, the intersection graphs of interior-disjoint simply-connected regions in the plane, are exactly the bipartite halves of planar graphs.[3]

See also

References

  1. ↑ Wilson, Robin J. (2004), Topics in Algebraic Graph Theory, Encyclopedia of Mathematics and its Applications, 102, Cambridge University Press, p. 188, ISBN 9780521801973.
  2. ↑ Chihara, Laura; Stanton, Dennis (1986), "Association schemes and quadratic transformations for orthogonal polynomials", Graphs and Combinatorics, 2 (2): 101–112, doi:10.1007/BF01788084, MR 932118.
  3. ↑ Chen, Zhi-Zhong; Grigni, Michelangelo; Papadimitriou, Christos H. (2002), "Map graphs", Journal of the ACM, 49 (2): 127–138, doi:10.1145/506147.506148, MR 2147819.
This article is issued from Wikipedia - version of the 10/1/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.