Clausen function
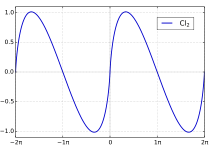
In mathematics, the Clausen function, introduced by Thomas Clausen (1832), is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other special functions. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function.
The Clausen function of order 2 – often referred to as the Clausen function, despite being but one of a class of many – is given by the integral:
In the range : the sine function inside the absolute value sign remains strictly positive, so the absolute value signs may be omitted. The Clausen function also has the Fourier series representation:
The Clausen functions, as a class of functions, feature extensively in many areas of modern mathematical research, particularly in relation to the evaluation of many classes of logarithmic and polylogarithmic integrals, both definite and indefinite. They also have numerous applications with regard to the summation of hypergeometric series, summations involving the inverse of the central binomial coefficient, sums of the polygamma function, and Dirichlet L-series.
Basic properties
The Clausen function (of order 2) has simple zeros at all (integer) multiples of : since if : is an integer, :
It has maxim at :
and minim at :
The following properties are immediate consequences of the series definition:
(Ref: See Lu and Perez, 1992, below for these results, although no proofs are given).
General definition
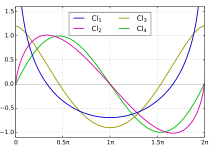
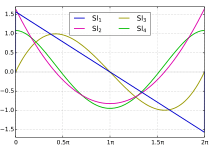
More generally, one defines the two generalized Clausen functions:
which are valid for complex z with Re z >1. The definition may be extended to all of the complex plane through analytic continuation.
When z is replaced with a non-negative integer, the Standard Clausen Functions are defined by the following Fourier series:
N.B. The SL-type Clausen functions have the alternative notation : and are sometimes referred to as the Glaisher-Clausen functions (after James Whitbread Lee Glaisher, hence the GL-notation).
Relation to the Bernoulli polynomials
The SL-type Clausen function are polynomials in , and are closely related to the Bernoulli polynomials. This connection is apparent from the Fourier series representations of the Bernoulli polynomials:
- .
- .
Setting in the above, and then rearranging the terms gives the following closed form (polynomial) expressions:
- ,
where the Bernoulli polynomials are defined in terms of the Bernoulli numbers by the relation:
Explicit evaluations derived from the above include:
Duplication formula
For :, the duplication formula can be proven directly from the Integral definition (see also Lu and Perez, 1992, below for the result – although no proof is given):
Immediate consequences of the duplication formula, along with use of the special value :, include the relations:
For higher order Clausen functions, duplication formulae can be obtained from the one given above; simply replace with the dummy variable , and integrate over the interval Applying the same process repeatedly yields:
And more generally, upon induction on
Use of the generalized duplication formula allows for an extension of the result for the Clausen function of order 2, involving Catalan's constant. For
Where is the Dirichlet beta function.
Proof of the duplication formula
From the integral definition,
Apply the duplication formula for the sine function, : to obtain
Apply the substitution on both integrals:
On that last integral, set , and use the trigonometric identity to show that:
Therefore,
Derivatives of general order Clausen functions
Direct differentiation of the Fourier series expansions for the Clausen functions give:
By appealing to the First Fundamental Theorem Of Calculus, we also have:
Relation to the inverse tangent integral
The inverse tangent integral is defined on the interval : by
It has the following closed form in terms of the Clausen Function:
Proof of the inverse tangent integral relation
From the integral definition of the inverse tangent integral, we have
Performing an integration by parts
Apply the substitution : to obtain
For that last integral, apply the transform : to get
Finally, as with the proof of the Duplication formula, the substitution reduces that last integral to
Thus
Relation to the Barnes' G-function
For real :, the Clausen function of second order can be expressed in terms of the Barnes G-function and (Euler) Gamma function:
Or equivalently
Ref: See Adamchik, "Contributions to the Theory of the Barnes function", below.
Relation to the polylogarithm
The Clausen functions represent the real and imaginary parts of the polylogarithm, on the unit circle:
This is easily seen by appealing to the series definition of the polylogarithm.
By Euler's theorem,
and by de Moivre's Theorem (De Moivre's formula)
Hence
Relation to the polygamma function
The Clausen functions are intimately connected to the polygamma function. Indeed, it is possible to express Clausen functions as linear combinations of sine functions and polygamma functions. One such relation is shown here, and proven below:
Let and be positive integers, such that is a rational number , then, by the series definition for the higher order Clausen function (of even index):
We split this sum into exactly p-parts, so that the first series contains all, and only, those terms congruent to the second series contains all terms congruent to etc., up to the final p-th part, that contain all terms congruent to
We can index these sums to form a double sum:
Applying the addition formula for the sine function, the sine term in the numerator becomes:
Consequently,
To convert the inner sum in the double sum into a non-alternating sum, split in two in parts in exactly the same way as the earlier sum was split into p-parts:
For , the polygamma function has the series representation
So, in terms of the polygamma function, the previous inner sum becomes:
Plugging this back into the double sum gives the desired result:
Relation to the generalized logsine integral
The generalized logsine integral is defined by:
In this generalized notation, the Clausen function can be expressed in the form:
Kummer's relation
Ernst Kummer and Rogers give the relation
valid for .
Relation to the Lobachevsky function
The Lobachevsky function Λ or Л is essentially the same function with a change of variable:
though the name "Lobachevsky function" is not quite historically accurate, as Lobachevsky's formulas for hyperbolic volume used the slightly different function
Relation to Dirichlet L-functions
For rational values of (that is, for for some integers p and q), the function can be understood to represent a periodic orbit of an element in the cyclic group, and thus can be expressed as a simple sum involving the Hurwitz zeta function. This allows relations between certain Dirichlet L-functions to be easily computed.
Series acceleration
A series acceleration for the Clausen function is given by
which holds for . Here, is the Riemann zeta function. A more rapidly convergent form is given by
Convergence is aided by the fact that approaches zero rapidly for large values of n. Both forms are obtainable through the types of resummation techniques used to obtain rational zeta series. (ref. Borwein, et al., 2000, below).
Special values
Some special values include
Generalized special values
Some special values for higher order Clausen functions include
where : is Catalan's constant, : is the Dirichlet beta function, : is the eta function (also called the alternating zeta function), and : is the Riemann zeta function.
Integrals of the direct function
The following integrals are easily proven from the series representations of the Clausen function:
Integral evaluations involving the direct function
A large number of trigonometric and logarithmo-trigonometric integrals can be evaluated in terms of the Clausen function, and various common mathematical constants like (Catalan's constant), , and the special cases of the zeta function, and .
The examples listed below follow directly from the integral representation of the Clausen function, and the proofs require little more than basic trigonometry, integration by parts, and occasional term-by-term integration of the Fourier series definitions of the Clausen functions.
References
- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 27.8". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C., USA; New York, USA: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 1005. ISBN 0-486-61272-4. LCCN 64-60036. MR 0167642. ISBN 978-0-486-61272-0. LCCN 65-12253.
- Clausen, Thomas (1832). "Über die Function sin φ + (1/22) sin 2φ + (1/32) sin 3φ + etc.". Journal für die reine und angewandte Mathematik. 8: 298–300. ISSN 0075-4102.
- Wood, Van E. (1968). "Efficient calculation of Clausen's integral". Math. Comp. 22 (104): 883–884. doi:10.1090/S0025-5718-1968-0239733-9. MR 0239733.
- Leonard Lewin, (Ed.). Structural Properties of Polylogarithms (1991) American Mathematical Society, Providence, RI. ISBN 0-8218-4532-2
- Lu, Hung Jung; Perez, Christopher A. (1992). "Massless one-loop scalar three-point integral and associated Clausen, Glaisher, and L-functions" (PDF).
- Kölbig, Kurt Siegfried (1995). "Chebyshev coefficients for the Clausen function Cl2(x)". J. Comput. Appl. Math. 64 (3): 295–297. doi:10.1016/0377-0427(95)00150-6. MR 1365432.
- Borwein, Jonathan M.; Bradley, David M.; Crandall, Richard E. (2000). "Computational Strategies for the Riemann Zeta Function" (PDF). J. Comp. App. Math. 121: 247–296. doi:10.1016/s0377-0427(00)00336-8. MR 1780051.
- Adamchik, Viktor. S. (2003). "Contributions to the Theory of the Barnes Function". arXiv:math/0308086v1
 .
. - Kalmykov, Mikahil Yu.; Sheplyakov, A. (2005). "LSJK – a C++ library for arbitrary-precision numeric evaluation of the generalized log-sine integral". Comput. Phys. Comm. 172: 45–59. doi:10.1016/j.cpc.2005.04.013. arXiv:hep-ph/0411100
- Borwein, Jonathan M.; Straub, Armin (2013). "Relations for Nielsen Polylogarithms". J. Approx. Theory. 193. pp. 74–88. doi:10.1016/j.jat.2013.07.003.
- Mathar, R. J. (2013). "A C99 implementation of the Clausen sums". arXiv:1309.7504
 .
.