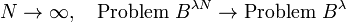Covector mapping principle

The covector mapping principle is a special case of Riesz' representation theorem, which is a fundamental theorem in functional analysis. The name was coined by Ross and co-workers,[1][2] [3][4][5][6] It provides conditions under which dualization can be commuted with discretization in the case of computational optimal control.

Description

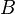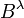An application of Pontryagin's minimum principle to Problem B , a given optimal control problem generates a boundary value problem. According to Ross, this boundary value problem is a Pontryagin lift and is represented as Problem B^\lambda.

Illustration of the Covector Mapping Principle (adapted from Ross and Fahroo .[7]

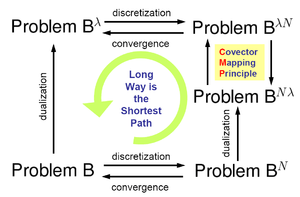
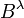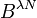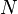Now suppose one discretizes Problem B^\lambda. This generates ProblemB^{\lambda N} where N represents the number of discrete pooints. For convergence, it is necessary to prove that as

N \to \infty, \quad \text{Problem } B^{\lambda N} \to \text{Problem } B^\lambda

In the 1960s Kalman and others [8] showed that solving Problem 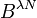B^{\lambda N} is extremely difficult. This difficulty, known as the curse of complexity,[9] is complementary to the curse of dimensionality.

In a series of papers starting in the late 1990s, Ross and Fahroo showed that one could arrive at a solution to Problem 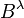B^{\lambda} (and hence Problem 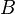B ) more easily by discretizing first (Problem 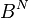B^{N}) and dualizing afterwards (Problem 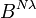B^{N \lambda}). The sequence of operations must be done carefully to ensure consistency and convergence. The covector mapping principle asserts that a covector mapping theorem can be discovered to map the solutions of Problem 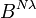B^{N \lambda} to Problem 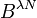B^{\lambda N} thus completing the circuit.

See also

References

  1. ↑ Ross, I. M., “A Historical Introduction to the Covector Mapping Principle,” Proceedings of the 2005 AAS/AIAA Astrodynamics Specialist Conference, August 7–11, 2005 Lake Tahoe, CA. AAS 05-332.
  2. ↑ Q. Gong, I. M. Ross, W. Kang, F. Fahroo, Connections between the covector mapping theorem and convergence of pseudospectral methods for optimal control, Computational Optimization and Applications, Vol. 41, pp. 307–335, 2008
  3. ↑ Ross, I. M. and Fahroo, F., “Legendre Pseudospectral Approximations of Optimal Control Problems,” Lecture Notes in Control and Information Sciences, Vol. 295, Springer-Verlag, New York, 2003, pp 327–342.
  4. ↑ Ross, I. M. and Fahroo, F., “Discrete Verification of Necessary Conditions for Switched Nonlinear Optimal Control Systems,” Proceedings of the American Control Conference, June 2004, Boston, MA
  5. ↑ Ross, I. M. and Fahroo, F., “A Pseudospectral Transformation of the Covectors of Optimal Control Systems,” Proceedings of the First IFAC Symposium on System Structure and Control, Prague, Czech Republic, 29–31 August 2001.
  6. ↑ W. Kang, I. M. Ross, Q. Gong, Pseudospectral optimal control and its convergence theorems, Analysis and Design of Nonlinear Control Systems, Springer, pp.109–124, 2008.
  7. ↑ I. M. Ross and F. Fahroo, A Perspective on Methods for Trajectory Optimization, Proceedings of the AIAA/AAS Astrodynamics Conference, Monterey, CA, August 2002. Invited Paper No. AIAA 2002-4727.
  8. ↑ Bryson, A.E. and Ho, Y.C. Applied optimal control. Hemisphere, Washington, DC, 1969.
  9. ↑ Ross, I. M. A Primer on Pontryagin's Principle in Optimal Control. Collegiate Publishers. Carmel, CA, 2009. ISBN 978-0-9843571-0-9.
This article is issued from Wikipedia - version of the 5/1/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.