Coxeter notation

Fundamental domains of reflective 3D point groups
, [ ]=[1] C_1v	, [2] C_2v	, [3] C_3v	, [4] C_4v	, [5] C_5v	, [6] C_6v
Order 2	Order 4	Order 6	Order 8	Order 10	Order 12
[2]=[2,1] D_1h	[2,2] D_2h	[2,3] D_3h	[2,4] D_4h	[2,5] D_5h	[2,6] D_6h
Order 4	Order 8	Order 12	Order 16	Order 20	Order 24
, [3,3], T_d		, [4,3], O_h		, [5,3], I_h
Order 24		Order 48		Order 120
Coxeter notation expresses Coxeter groups as a list of branch orders of a Coxeter diagram, like the polyhedral groups, = [p,q]. dihedral groups, , can be expressed a product [ ]×[n] or in a single symbol with an explicit order 2 branch, [2,n].

In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group in a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter, and has been more comprehensively defined by Norman Johnson.

Reflectional groups

Further information: Point group

For Coxeter groups defined by pure reflections, there is a direct correspondence between the bracket notation and Coxeter-Dynkin diagram. The numbers in the bracket notation represent the mirror reflection orders in the branches of the Coxeter diagram. It uses the same simplification, suppressing 2s between orthogonal mirrors.

The Coxeter notation is simplified with exponents to represent the number of branches in a row for linear diagram. So the A_n group is represented by [3^n-1], to imply n nodes connected by n-1 order-3 branches. Example A₂ = [3,3] = [3²] or [3^1,1] represents diagrams or .

Coxeter initially represented bifurcating diagrams with vertical positioning of numbers, but later abbreviated with an exponent notation, like [3^p,q,r], starting with [3^1,1,1] = as D₄. Coxeter allowed for zeros as special cases to fit the A_n family, like A₃ = [3,3,3,3] = [3^4,0,0] = [3^3,1,0] = [3^2,2,0], like = = .

Coxeter groups formed by cyclic diagrams are represented by parenthesese inside of brackets, like [(p,q,r)] = for the triangle group (p q r). If the branch orders are equal, they can be grouped as an exponent as the length the cycle in brackets, like [(3,3,3,3)] = [3^[4]], representing Coxeter diagram or . can be represented as [3,(3,3,3)] or [3,3^[3]].

More complicated looping diagrams can also be expressed with care. The paracompact Coxeter group can be represented by Coxeter notation [(3,3,(3),3,3)], with nested/overlapping parentheses showing two adjacent [(3,3,3)] loops, and is also represented more compactly as [3^[ ]×[ ]], representing the rhombic symmetry of the Coxeter diagram. The paracompact complete graph diagram or , is represented as [3^[3,3]] with the superscript [3,3] as the symmetry of its regular tetrahedron coxeter diagram.

The Coxeter diagram usually leaves order-2 branches undrawn, but the bracket notation includes an explicit 2 to connect the subgraphs. So the Coxeter diagram = A₂×A₂ = 2A₂ can be represented by [3]×[3] = [3]² = [3,2,3].

Finite groups
Rank	Group symbol	Bracket notation	Coxeter diagram
2	A₂	[3]
2	B₂	[4]
2	H₂	[5]
2	G₂	[6]
2	I₂(p)	[p]
3	I_h, H₃	[5,3]
3	T_d, A₃	[3,3]
3	O_h, B₃	[4,3]
4	A₄	[3,3,3]
4	B₄	[4,3,3]
4	D₄	[3^1,1,1]
4	F₄	[3,4,3]
4	H₄	[5,3,3]
n	A_n	[3^n-1]	..
n	B_n	[4,3^n-2]	...
n	D_n	[3^n-3,1,1]	...
6	E₆	[3^2,2,1]
7	E₇	[3^3,2,1]
8	E₈	[3^4,2,1]

Affine groups
Group symbol	Bracket notation	Coxeter diagram
${\tilde {I}}_{1}$	[∞]
${\tilde {A}}_{2}$	[3^[3]]
${\tilde {C}}_{2}$	[4,4]
${\tilde {G}}_{2}$	[6,3]
${\tilde {A}}_{3}$	[3^[4]]
${\tilde {B}}_{3}$	[4,3^1,1]
${\tilde {C}}_{3}$	[4,3,4]
${{\tilde {A}}}_{4}$	[3^[5]]
${\tilde {B}}_{4}$	[4,3,3^1,1]
${{\tilde {C}}}_{4}$	[4,3,3,4]
${\tilde {D}}_{4}$	[ 3^1,1,1,1]
${\tilde {F}}_{4}$	[3,4,3,3]
${\tilde {A}}_{n}$	[3^[n+1]]	... or ...
${\tilde {B}}_{n}$	[4,3^n-2,3^1,1]	...
${\tilde {C}}_{n}$	[4,3^n-1,4]	...
${\tilde {D}}_{n}$	[ 3^1,1,3^n-3,3^1,1]	...
${\tilde {E}}_{6}$	[3^2,2,2]
${\tilde {E}}_{7}$	[3^3,3,1]
${\tilde {E}}_{8}$	[3^5,2,1]

Compact Hyperbolic groups
Group symbol	Bracket notation	Coxeter diagram
	[p,q] with 2(p+q)<pq
	[(p,q,r)] with p+q+r>9
${\overline {BH}}_{3}$	[4,3,5]
${\overline {K}}_{3}$	[5,3,5]
${\overline {J}}_{3}$	[3,5,3]
${\overline {DH}}_{3}$	[5,3^1,1]
${\widehat {AB}}_{3}$	[(3,3,3,4)]
${\widehat {AH}}_{3}$	[(3,3,3,5)]
${\widehat {BB}}_{3}$	[(3,4,3,4)]
${\widehat {BH}}_{3}$	[(3,4,3,5)]
${\widehat {HH}}_{3}$	[(3,5,3,5)]
${\overline {H}}_{4}$	[3,3,3,5]
${\overline {BH}}_{4}$	[4,3,3,5]
${\overline {K}}_{4}$	[5,3,3,5]
${\overline {DH}}_{4}$	[5,3,3^1,1]
${\widehat {AF}}_{4}$	[(3,3,3,3,4)]

For the affine and hyperbolic groups, the subscript is one less than the number of nodes in each case, since each of these groups was obtained by adding a node to a finite group's diagram.

Subgroups

Coxeter's notation represents rotational/translational symmetry by adding a ⁺ superscript operator outside the brackets which cuts the order of the group in half (called index 2 subgroup). This is called a direct subgroup because what remains are only direct isometries without reflective symmetry.

⁺ operators can also be applied inside of the brackets, and creates "semidirect" subgroups that include both reflective and nonreflective generators. Semidirect subgroups can only apply to Coxeter group subgroups that have even order branches next to it. Elements by parentheses inside of a Coxeter group can be give a ⁺ superscript operator, having the effect of dividing adjacent ordered branches into half order, thus is usually only applied with even numbers. For example, [4,3⁺] () and [4,(3,3)⁺] (). The subgroup index is 2ⁿ for n ⁺ operators.

Groups without neighboring ⁺ elements can be seen in ringed nodes Coxeter-Dynkin diagram for uniform polytopes and honeycomb are related to hole nodes around the ⁺ elements, empty circles with the alternated nodes removed. So the snub cube, has symmetry [4,3]⁺ (), and the snub tetrahedron, has symmetry [4,3⁺] (), and a demicube, h{4,3} = {3,3} ( or = ) has symmetry [1⁺,4,3] = [3,3] ( or = = ).

Halving subgroups

Example halving operations

[ 1,4, 1] = [4]	= = [1⁺,4, 1]=[2]=[ ]×[ ]

= = [ 1,4,1⁺]=[2]=[ ]×[ ]	= = = [1⁺,4,1⁺] = [2]⁺

Johnson extends the ⁺ operator to work with a placeholder 1 nodes, which removes mirrors, doubling the size of the fundamental domain and cuts the group order in half. In general this operation only applies to mirrors bounded by all even-order branches. The 1 represents a mirror so [2p] can be seen as [2p,1], [1,2p], or [1,2p,1], like diagram or , with 2 mirrors related by an order-2p dihedral angle. The effect of a mirror removal is to duplicate connecting nodes, which can be seen in the Coxeter diagrams: = , or in bracket notation:[1⁺,2p, 1] = [1,p,1] = [p].

Each of these mirrors can be removed so h[2p] = [1⁺,2p,1] = [1,2p,1⁺] = [p], a reflective subgroup index 2. This can be shown in a Coxeter diagram by adding a ⁺ symbol above the node: = = .

If both mirrors are removed, a quarter subgroup is generated, with the branch order becoming a gyration point of half the order:

q[2p] = [1⁺,2p,1⁺] = [p]⁺, a rotational subgroup of index 4.

For example, (with p=2): [4,1⁺] = [1⁺,4] = [2] = [ ]×[ ], order 4. [1⁺,4,1⁺] = [2]⁺, order 2.

The opposite to halving is doubling which adds a mirror, bisecting a fundamental domain, and doubling the group order.

p = [2p]

Halving operations apply for higher rank groups, like h[4,3] = [1⁺,4,3] = [3,3], removing half the mirrors at the 4-branch. The effect of a mirror removal is to duplicate all connecting nodes, which can be seen in the Coxeter diagrams: = , h[2p,3] = [1⁺,2p,3] = [(p,3,3)].

Doubling by adding a mirror also applies in reversing the halving operation: 3,3 = [4,3], or more generally (q,q,p) = [2p,q].

Tetrahedral symmetry	Octahedral symmetry
T_d, [3,3] = [1⁺,4,3] = = (Order 24)	O_h, [4,3] = 3,3 (Order 48)

Radical subgroups

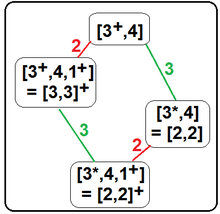
A radical subgroup is similar to an alternation, but removes the rotational generators.

Johnson also added an asterisk or star * operator, that acts similar to the ⁺ operator, but removes rotational symmetry. The index of the radical subgroup is the order of the removed element. For example, [4,3*] ≅ [2,2]. The removed [3] subgroup is order 6 so [2,2] is an index 6 subgroup of [4,3].

The radical subgroups represent the inverse operation to an extended symmetry operation. For example, [4,3*] ≅ [2,2], and in reverse [2,2] can be extended as [3[2,2]] ≅ [4,3]. The subgroups can be expressed as a Coxeter diagram: ≅ . The removed node (mirror) causes adjacent mirror virtual mirrors to become real mirrors.

If [4,3] has generators {0,1,2}, [4,3⁺], index 2, has generators {0,12}; [1⁺,4,3], index 2 has generators {010,1,2}; while radical subgroup [4,3*], index 6, has generators {01210, 2, (012)³}; and finally [1⁺,4,3*], index 12 has generators {0(12)²0, (012)²01}.

Trionic subgroups

[3,3]^⅄ ≅ [2⁺,4] as one of 3 sets of 2 orthogonal mirrors in stereographic projection. The red, green, and blue represent 3 sets of mirrors, and the gray lines are removed mirrors, leaving 2-fold gyrations (purple diamonds).

Trionic relations of [3,3]

Johnson identified two specific subgroups of [3,3], first an index 3 subgroup [3,3]^⅄ ≅ [2⁺,4], with [3,3] ( = ) generators {0,1,2}. It can also be written as [(3,3,2^⅄)] (^⅄) as a reminder of its generators {02,1}. This symmetry reduction is the relationship between the regular tetrahedron and the tetragonal disphenoid, represent a stretching of a tetrahedron perpendicular to two opposite edges.

Secondly he identifies a related index 6 subgroup [3,3]^Δ or [(3,3,2^⅄)]⁺, index 3 from [3,3]⁺ ≅ [2,2]⁺, with generators {02,1021}, from [3,3] and its generators {0,1,2}.

These subgroups also apply within larger Coxeter groups with [3,3] subgroup with neighboring branches all even order.

Trionic subgroup relations of [3,3,4]

For example, [(3,3)⁺,4], [(3,3)^⅄,4], and [(3,3)^Δ,4] are subgroups of [3,3,4], index 2, 3 and 6 respectively. The generators of [(3,3)^⅄,4] ≅ 4,2,4 ≅ [8,2⁺,8], order 128, are {02,1,3} from [3,3,4] generators {0,1,2,3}. And [(3,3)^Δ,4] ≅ [[4,2<sup>+</sup>,4]], order 64, has generators {02,1021,3}.

Also related [3^1,1,1] = [3,3,4,1⁺] has trionic subgroups: [3^1,1,1]^⅄ = [(3,3)^⅄,4,1⁺], order 64, and [3^1,1,1]^Δ = [(3,3)^Δ,4,1⁺] ≅ [[4,2<sup>+</sup>,4]]⁺, order 32.

Central inversion

A 2D central inversion is a 180 degree rotation, [2]⁺

A central inversion, order 2, is operationally differently by dimension. The group [ ]ⁿ = [2^n-1] represents n orthogonal mirrors in n-dimensional space, or an n-flat subspace of a higher dimensional space. The mirrors of the group [2^n-1] are numbered 0..n-1. The order of the mirrors doesn't matter in the case of an inversion.

From that basis, the central inversion has a generator as the product of all the orthogonal mirrors. In Coxeter notation this inversion group is expressed by adding an alternation ⁺ to each 2 branch. The alternation symmetry is marked on Coxeter diagram nodes as open nodes.

A Coxeter-Dynkin diagram can be marked up with explicit 2 branches defining a linear sequence of mirrors, open-nodes, and shared double-open nodes to show the chaining of the reflection generators.

For example, [2⁺,2] and [2,2⁺] are subgroups index 2 of [2,2], , and are represented as and with generators {01,2} and {0,12} respectively. Their common subgroup index 4 is [2⁺,2⁺], and is represented by , with the double-open marking a shared node in the two alternations, and a single rotoreflection generator {012}.

Dimension	Coxeter notation	Order	Operation	Generator
2	[2]⁺	2	180° rotation, C₂	{01}
3	[2⁺,2⁺]	2	rotoreflection, C_i or S₂	{012}
4	[2⁺,2⁺,2⁺]	2	double rotation	{0123}
5	[2⁺,2⁺,2⁺,2⁺]	2	double rotary reflection	{01234}
6	[2⁺,2⁺,2⁺,2⁺,2⁺]	2	triple rotation	{012345}
7	[2⁺,2⁺,2⁺,2⁺,2⁺,2⁺]	2	triple rotary reflection	{0123456}

Rotations and rotary reflections

Rotations and rotary reflections are constructed by a single single-generator product of all the reflections of a prismatic group, [2p]×[2q]×... When gcd(p,q,..)=1, they are isomorphic to the abstract cyclic group Z_n, of order n=2pq.

The 4-dimensional double rotations, [2p⁺,2⁺,2q⁺], which include a central group, and are expressed by Conway as ±[C_p×C_q], order 2pq/gcd(p,q).^[1]

Dimension	Coxeter notation	Order	Operation	Generator	Direct subgroup
2	[p]⁺	p	Rotation	{01}	[p]⁺
3	[2p⁺,2⁺]	2p	rotary reflection	{012}
4	[2p⁺,2⁺,2⁺]		double rotation	{0123}
5	[2p⁺,2⁺,2⁺,2⁺]		double rotary reflection	{01234}
6	[2p⁺,2⁺,2⁺,2⁺,2⁺]		triple rotation	{012345}
7	[2p⁺,2⁺,2⁺,2⁺,2⁺,2⁺]		triple rotary reflection	{0123456}
4	[2p⁺,2⁺,2q⁺]	2pq	double rotation	{0123}	[p⁺,2,q⁺]
5	[2p⁺,2⁺,2q⁺,2⁺]		double rotary reflection	{01234}
6	[2p⁺,2⁺,2q⁺,2⁺,2⁺]		triple rotation	{012345}
7	[2p⁺,2⁺,2q⁺,2⁺,2⁺,2⁺]		triple rotary reflection	{0123456}
6	[2p⁺,2⁺,2q⁺,2⁺,2r⁺]	2pqr	triple rotation	{012345}	[p⁺,2,q⁺,2,r⁺]
7	[2p⁺,2⁺,2q⁺,2⁺,2r⁺,2⁺]	2pqr	triple rotary reflection	{0123456}	[p⁺,2,q⁺,2,r⁺]

Commutator subgroups

Simple groups with only odd-order branch elements have only a single rotational/translational subgroup of order 2, which is also the commutator subgroup, examples [3,3]⁺, [3,5]⁺, [3,3,3]⁺, [3,3,5]⁺. For other Coxeter groups with even-order branches, the commutator subgroup has index 2^c, where c is the number of disconnected subgraphs when all the even-order branches are removed.^[2] For example, [4,4] has three independent nodes in the Coxeter diagram when the 4s are removed, so its commutator subgroup is index 2³, and can have different representations, all with three ⁺ operators: [4⁺,4⁺]⁺, [1⁺,4,1⁺,4,1⁺], [1⁺,4,4,1⁺]⁺, or [(4⁺,4⁺,2⁺)]. A general notation can be used with +c as a group exponent, like [4,4]⁺³.

Example subgroups

Rank 2 example subgroups

Dihedral symmetry groups with even-orders have a number of subgroups. This example shows two generator mirrors of [4] in red and green, and looks at all subgroups by halfing, rank-reduction, and their direct subgroups. The group [4], has two mirror generators 0, and 1. Each generate two virtual mirrors 101 and 010 by reflection across the other.

Subgroups of [4]
Index	1	2 (half)		4 (Rank-reduction)
Diagram
Coxeter	[1,4,1] = [4]	= = [1⁺,4,1] = [1⁺,4] = [2]	= = [1,4,1⁺] = [4,1⁺] = [2]	[1] = [ ]	[1] = [ ]
Generators	{0,1}	{101,1}	{0,010}	{0}	{1}
Direct subgroups
Index	2	4		8
Diagram
Coxeter	[4]⁺	= = = [4]⁺² = [1⁺,4,1⁺] = [2]⁺		[ ]⁺
Generators	{01}	{(01)²}		{0²} = {1²} = {(01)⁴} = { }

Rank 3 Euclidean example subgroups

The [4,4] group has 15 small index subgroups. This table shows them all, with a yellow fundamental domain for pure reflective groups, and alternating white and blue domains which are paired up to make rotational domains. Cyan, red, and green mirror lines correspond to the same colored nodes in the Coxeter diagram. Subgroup generators can be expressed as products of the original 3 mirrors of the fundamental domain, {0,1,2}, corresponding to the 3 nodes of the Coxeter diagram, . A product of two intersecting reflection lines makes a rotation, like {012}, {12}, or {02}. Removing a mirror causes two copies of neighboring mirrors, across the removed mirror, like {010}, and {212}. Two rotations in series cut the rotation order in half, like {0101} or {(01)²}, {1212} or {(02)²}. A product of all three mirrors creates a transreflection, like {012} or {120}.

Small index subgroups of [4,4]
Index	1	2			4
Diagram
Coxeter	[1,4,1,4,1] = [4,4]	[1⁺,4,4] =	[4,4,1⁺] =	[4,1⁺,4] =	[1⁺,4,4,1⁺] =	[4⁺,4⁺]
Generators	{0,1,2}	{010,1,2}	{0,1,212}	{0,101,121,2}	{010,1,212,20102}	{(01)²,(12)²,012,120}
Orbifold	*442			*2222		22×
Semidirect subgroups
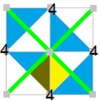
Index		2			4
Diagram
Coxeter		[4,4⁺]	[4⁺,4]	[(4,4,2⁺)] =	[4,1⁺,4,1⁺] = =	[1⁺,4,1⁺,4] = =
Generators		{0,12}	{01,2}	{02,1,212}	{0,101,(12)²}	{(01)²,121,2}
Orbifold		4*2		2*22
Direct subgroups
Index	2	4			8
Diagram
Coxeter	[4,4]⁺ =	[4,4⁺]⁺ =	[4⁺,4]⁺ =	[(4,4,2⁺)]⁺ =	[4,4]⁺³ = [(4⁺,4⁺,2⁺)] = [1⁺,4,1⁺,4,1⁺] = [4⁺,4⁺]⁺ = = = =
Generators	{01,12}	{(01)²,12}	{01,(12)²}	{02,(01)²,(12)²}	{(01)²,(12)²,2(01)²2}
Orbifold	442			2222
Radical subgroups
Index		8		16
Diagram
Coxeter		[4,4*] =	[4*,4] =	[4,4*]⁺ =	[4*,4]⁺ =
Orbifold		*2222		2222

Hyperbolic example subgroups

The same set of 15 small subgroups exists on all triangle groups with even order elements, like [6,4] in the hyperbolic plane:

Small index subgroups of [6,4]
Index	1	2			4
Diagram
Coxeter	[1,6,1,4,1] = [6,4]	[1⁺,6,4] =	[6,4,1⁺] =	[6,1⁺,4] =	[1⁺,6,4,1⁺] =	[6⁺,4⁺]
Generators	{0,1,2}	{010,1,2}	{0,1,212}	{0,101,121,2}	{010,1,212,20102}	{(01)²,(12)²,012}
Orbifold	*642	*443	*662	*3222	*3232	32×
Semidirect subgroups
Diagram
Coxeter		[6,4⁺]	[6⁺,4]	[(6,4,2⁺)]	[6,1⁺,4,1⁺] = = = =	[1⁺,6,1⁺,4] = = = =
Generators		{0,12}	{01,2}	{02,1,212}	{0,101,(12)²}	{(01)²,121,2}
Orbifold		4*3	6*2	2*32	2*33	3*22
Direct subgroups
Index	2	4			8
Diagram
Coxeter	[6,4]⁺ =	[6,4⁺]⁺ =	[6⁺,4]⁺ =	[(6,4,2⁺)]⁺ =	[6⁺,4⁺]⁺ = [1⁺,6,1⁺,4,1⁺] = = =
Generators	{01,12}	{(01)²,12}	{01,(12)²}	{02,(01)²,(12)²}	{(01)²,(12)²,201012}
Orbifold	642	443	662	3222	3232
Radical subgroups
Index		8	12	16	24
Diagram
Coxeter (orbifold)		[6,4] = (3333)	[6,4] (222222)	[6,4*]⁺ = (3333)	[6*,4]⁺ (222222)

Extended symmetry

Wallpaper group	Triangle symmetry	Extended symmetry	Extended diagram	Extended group	Honeycombs
p3m1 (*333)	a1	[3^[3]]		${\tilde {A}}_{2}$	(none)
p6m (*632)	i2	[[3^[3]]] ↔ [6,3]	↔	${\tilde {A}}_{2}$ ×2 ↔ ${\tilde {G}}_{2}$	₁, ₂
p31m (3*3)	g3	[3⁺[3^[3]]] ↔ [6,3⁺]		${\tilde {A}}_{2}$ ×3 ↔ ½ ${\tilde {G}}_{2}$	(none)
p6 (632)	r6	[3[3^[3]]]⁺ ↔ [6,3]⁺	↔	½ ${\tilde {A}}_{2}$ ×6 ↔ ½ ${\tilde {G}}_{2}$	₍₁₎
p6m (*632)	r6	[3[3^[3]]] ↔ [6,3]	↔	${\tilde {A}}_{2}$ ×6 ↔ ${\tilde {G}}_{2}$	₃

In the Euclidean plane, the

{\tilde {A}}_{2}

, [3^[3]] Coxeter group can be extended in two ways into the

{\tilde {G}}_{2}

, [6,3] Coxeter group and relates uniform tilings as ringed diagrams.

Coxeter's notation includes double square bracket notation, X to express automorphic symmetry within a Coxeter diagram. Johnson added alternative of angled-bracket <[X]> option as equivalent to square brackets for doubling to distinguish diagram symmetry through the nodes versus through the branches. Johnson also added a prefix symmetry modifier [Y[X]], where Y can either represent symmetry of the Coxeter diagram of [X], or symmetry of the fundamental domain of [X].

For example, in 3D these equivalent rectangle and rhombic geometry diagrams of ${\tilde {A}}_{3}$ : and , the first doubled with square brackets, [[3^[4]]] or twice doubled as [2[3^[4]]], with [2], order 4 higher symmetry. To differentiate the second, angled brackets are used for doubling, <[3^[4]]> and twice doubled as <2[3^[4]]>, also with a different [2], order 4 symmetry. Finally a full symmetry where all 4 nodes are equivalent can be represented by [4[3^[4]]], with the order 8, [4] symmetry of the square. But by considering the tetragonal disphenoid fundamental domain the [4] extended symmetry of the square graph can be marked more explicitly as [(2⁺,4)[3^[4]]] or [2⁺,4[3^[4]]].

Further symmetry exists in the cyclic ${\tilde {A}}_{n}$ and branching $D_{3}$ , ${\tilde {E}}_{6}$ , and ${\tilde {D}}_{4}$ diagrams. ${\tilde {A}}_{n}$ has order 2n symmetry of a regular n-gon, {n}, and is represented by [n[3^[n]]]. $D_{3}$ and ${\tilde {E}}_{6}$ are represented by [3[3^1,1,1]] = [3,4,3] and [3[3^2,2,2]] respectively while ${\tilde {D}}_{4}$ by [(3,3)[3^1,1,1,1]] = [3,3,4,3], with the diagram containing the order 24 symmetry of the regular tetrahedron, {3,3}. The paracompact hyperbolic group ${\bar {L}}_{5}$ = [3^1,1,1,1,1], , contains the symmetry of a 5-cell, {3,3,3}, and thus is represented by [(3,3,3)[3^1,1,1,1,1]] = [3,4,3,3,3].

An asterisk * superscript is effectively an inverse operation, creating radical subgroups removing connected of odd-ordered mirrors.^[3]

Examples:

Example Extended groups and radical subgroups

Extended groups	Radical subgroups	Coxeter diagrams	Index
[3[2,2]] = [4,3]	[4,3*] = [2,2]	=	6
[(3,3)[2,2,2]] = [4,3,3]	[4,(3,3)*] = [2,2,2]	=	24
[1[3^1,1]] = 3,3 = [3,4]	[3,4,1⁺] = [3,3]	=	2
[3[3^1,1,1]] = [3,4,3]	[3*,4,3] = [3^1,1,1]	=	6
[2[3^1,1,1,1]] = [4,3,3,4]	[1⁺,4,3,3,4,1⁺] = [3^1,1,1,1]	=	4
[3[3,3^1,1,1]] = [3,3,4,3]	[3*,4,3,3] = [3^1,1,1,1]	=	6
[(3,3)[3^1,1,1,1]] = [3,4,3,3]	[3,4,(3,3)*] = [3^1,1,1,1]	=	24
[2[3,3^1,1,1,1]] = [3,(3,4)^1,1]	[3,(3,4,1⁺)^1,1] = [3,3^1,1,1,1]	=	4
[(2,3)[^1,13^1,1,1]] = [4,3,3,4,3]	[1⁺,4,3,3,4,3⁺] = [3^1,1,1,1,1]	=	12
[(3,3)[3,3^1,1,1,1]] = [3,3,4,3,3]	[3,3,4,(3,3)*] = [3^1,1,1,1,1]	=	24
[(3,3,3)[3^1,1,1,1,1]] = [3,4,3,3,3]	[3,4,(3,3,3)*] = [3^1,1,1,1,1]	=	120

Extended groups	Radical subgroups	Coxeter diagrams	Index
[1[3^[3]]] = [3,6]	[3,6,1⁺] = [3^[3]]	=	2
[3[3^[3]]] = [6,3]	[6,3*] = [3^[3]]	=	6
[1[3,3^[3]]] = [3,3,6]	[3,3,6,1⁺] = [3,3^[3]]	=	2
[(3,3)[3^[3,3]]] = [6,3,3]	[6,(3,3)*] = [3^[3,3]]	=	24
[1[∞]²] = [4,4]	[4,1⁺,4] = [∞]² = [∞]×[∞] = [∞,2,∞]	=	2
[2[∞]²] = [4,4]	[1⁺,4,4,1⁺] = [(4,4,2*)] = [∞]²	=	4
[4[∞]²] = [4,4]	[4,4*] = [∞]²	=	8
[2[3^[4]]] = [4,3,4]	[1⁺,4,3,4,1⁺] = [(4,3,4,2*)] = [3^[4]]	= =	4
[3[∞]³] = [4,3,4]	[4,3*,4] = [∞]³ = [∞,2,∞,2,∞]	=	6
[(3,3)[∞]³] = [4,3^1,1]	[4,(3^1,1)*] = [∞]³	=	24
[(4,3)[∞]³] = [4,3,4]	[4,(3,4)*] = [∞]³	=	48
[(3,3)[∞]⁴] = [4,3,3,4]	[4,(3,3)*,4] = [∞]⁴	=	24
[(4,3,3)[∞]⁴] = [4,3,3,4]	[4,(3,3,4)*] = [∞]⁴	=	384

Looking at generators, the double symmetry is seen as adding a new operator that maps symmetric positions in the Coxeter diagram, making some original generators redundant. For 3D space groups, and 4D point groups, Coxeter defines an index two subgroup of X, [[X]⁺], which he defines as the product of the original generators of [X] by the doubling generator. This looks similar to X⁺, which is the chiral subgroup of X. So for example the 3D space groups 4,3,4⁺ (I432, 211) and [[4,3,4]⁺] (Pm3n, 223) are distinct subgroups of 4,3,4 (Im3m, 229).

Computation with reflection matrices as symmetry generators

A Coxeter group, represented by Coxeter diagram , is given Coxeter notation [p,q] for the branch orders. Each node in the Coxeter diagram represents a mirror, by convention called ρ_i (and matrix R_i). The generators of this group [p,q] are reflections: ρ₀, ρ₁, and ρ₂. Rotational subsymmetry is given as products of reflections: By convention, σ_0,1 (and matrix S_0,1) = ρ₀ρ₁ represents a rotation of angle π/p, and σ_1,2 = ρ₁ρ₂ is a rotation of angle π/q, and σ_0,2 = ρ₀ρ₂ represents a rotation of angle π/2.

[p,q]⁺ is an index 2 subgroup represented by two rotation generators, each a products of two reflections: σ_0,1, σ_1,2, and representing rotations of π/p, and π/q angles respectively.

If q is even, [p⁺,q] is another subgroup of index 2, represented by rotation generator σ_0,1, and reflectional ρ₂.

If both p and q are even, [p⁺,q⁺] is a subgroup of index 4 with two generators, constructed as a product of all three reflection matrices: By convention as: ψ_0,1,2 and ψ_1,2,0, which are rotary reflections, representing a reflection and rotation or reflection.

In the case of affine Coxeter groups like , or , one mirror, usually the last, is translated off the origin. A translation generator τ_0,1 (and matrix T_0,1) is constructed as the product of two (or an even number of) reflections, including the affine reflection. A transreflection (reflection plus a translation) can be the product of an odd number of reflections φ_0,1,2 (and matrix V_0,1,2), like the index 4 subgroup : [4⁺,4⁺] = .

Another composite generator, by convention as ζ (and matrix Z), represents the inversion, mapping a point to its inverse. For [4,3] and [5,3], ζ = (ρ₀ρ₁ρ₂)^h/2, where h is 6 and 10 respectively, the Coxeter number for each family. For 3D Coxeter group [p,q] (), this subgroup is a rotary reflection [2⁺,h⁺].

Example, in 2D, the Coxeter group [p] () is represented by two reflection matrices R₀ and R₁, The cyclic symmetry [p]⁺ () is represented by rotation generator of matrix S_0,1.

R₀	R₁	S_0,1=R₀xR₁
$\left[{\begin{smallmatrix}1&0\\0&-1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p\\\sin 2\pi /p&-\cos 2\pi /p\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}\cos 2\pi /p&\sin 2\pi /p\\-\sin 2\pi /p&\cos 2\pi /p\\\end{smallmatrix}}\right]$

A simple example affine group is [4,4] () (p4m), can be given by three reflection matrices, constructed as a reflection across the x axis (y=0), a diagonal (x=y), and the affine reflection across the line (x=1). [4,4]⁺ () (p4) is generated by S_0,1 S_1,2, and S_0,2. [4⁺,4⁺] () (pgg) is generated by 2-fold rotation S_0,2 and transreflection V_0,1,2. [4⁺,4] () (p4g) is generated by S_0,1 and R₃. The group [(4,4,2⁺)] () (cmm), is generated by 2-fold rotation S_1,3 and reflection R₂.

R₀	R₁	R₂	S_0,1	S_1,2	S_0,2	V_0,1,2
$\left[{\begin{smallmatrix}1&0&0\\0&-1&0\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}0&1&0\\1&0&0\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}-1&0&2\\0&1&0\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}0&1&0\\-1&0&0\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}0&1&0\\-1&0&2\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}-1&0&2\\0&-1&0\\0&0&1\\\end{smallmatrix}}\right]$	$\left[{\begin{smallmatrix}0&1&0\\1&0&-2\\0&0&1\\\end{smallmatrix}}\right]$

Coxeter groups are categorized by their rank, being the number of nodes in its Coxeter-Dynkin diagram. The structure of the groups are also given with their abstract group types: In this article, the abstract dihedral groups are represented as Dih_n, and cyclic groups are represented by Z_n, with Dih₁=Z₂.

Rank one groups

Further information: One-dimensional symmetry group

In one dimension, the bilateral group [ ] represents a single mirror symmetry, abstract Dih₁ or Z₂, symmetry order 2. It is represented as a Coxeter–Dynkin diagram with a single node, . The identity group is the direct subgroup [ ]⁺, Z₁, symmetry order 1. The + superscript simply implies that alternate mirror reflections are ignored, leaving the identity group in this simplest case. Coxeter used a single open node to represent an alternation, .

Group	Coxeter notation	Coxeter diagram	Order	Description
C₁	[ ]⁺		1	Identity
D₁	[ ]		2	Reflection group

Rank two groups

Further information: Point groups in two dimensions

A regular hexagon, with markings on edges and vertices has 8 symmetries: [6], [3], [2], [1], [6]⁺, [3]⁺, [2]⁺, [1]⁺, with [3] and [1] existing in two forms, depending whether the mirrors are on the edges or vertices.

In two dimensions, the rectangular group [2], abstract D₁² or D₂, also can be represented as a direct product [ ]×[ ], being the product of two bilateral groups, represents two orthogonal mirrors, with Coxeter diagram, , with order 4. The 2 in [2] comes from linearization of the orthogonal subgraphs in the Coxeter diagram, as , with explicit branch order 2. The rhombic group, [2]⁺ (), half of the rectangular group, the point reflection symmetry, Z₂, order 2.

Coxeter notation to allow a 1 place-holder for lower rank groups, so [1] is the same as [ ], and [1⁺] or [1]⁺ is the same as [ ]⁺ and Coxeter diagram .

The full p-gonal group [p], abstract dihedral group D_p, (nonabelian for p>2), of order 2p, is generated by two mirrors at angle π/p, represented by Coxeter diagram . The p-gonal subgroup [p]⁺, cyclic group Z_p, of order p, generated by a rotation angle of π/p.

Coxeter notation uses double-bracking to represent an automorphic doubling of symmetry by adding a bisecting mirror to the fundamental domain. For example [[p]] adds a bisecting mirror to [p], and is isomorphic to [2p].

In the limit, going down to one dimensions, the full apeirogonal group is obtained when the angle goes to zero, so [∞], abstractly the infinite dihedral group D_∞, represents two parallel mirrors and has a Coxeter diagram . The apeirogonal group [∞]⁺, , abstractly the infinite cyclic group Z_∞, isomorphic to the additive group of the integers, is generated by a single nonzero translation.

In the hyperbolic plane, there is a full pseudogonal group [iπ/λ], and pseudogonal subgroup [iπ/λ]⁺, . These groups exist in regular infinite-sided polygons, with edge length λ. The mirrors are all orthogonal to a single line.

Example rank 2 finite and hyperbolic symmetries
Type	Finite					Affine	Hyperbolic
Geometry					...
Coxeter	[ ]	= [2]=[ ]×[ ]	[3]	[4]	[p]	[∞]	[∞]	[iπ/λ]
Order	2	4	6	8	2p	∞
Mirror lines are colored to correspond to Coxeter diagram nodes. Fundamental domains are alternately colored.
Even images (direct)					...
Odd images (inverted)					...
Coxeter	[ ]⁺	[2]⁺	[3]⁺	[4]⁺	[p]⁺	[∞]⁺	[∞]⁺	[iπ/λ]⁺
Order	1	2	3	4	p	∞
Cyclic subgroups represent alternate reflections, all even (direct) images.

Group	Intl	Orbifold	Coxeter	Order	Description
Finite
Z_n	n	n•	[n]⁺	n	Cyclic: n-fold rotations. Abstract group Z_n, the group of integers under addition modulo n.
D_n	nm	*n•	[n]	2n	Dihedral: cyclic with reflections. Abstract group Dih_n, the dihedral group.
Affine
Z_∞	∞	∞•	[∞]⁺	∞	Cyclic: apeirogonal group. Abstract group Z_∞, the group of integers under addition.
Dih_∞	∞m	*∞•	[∞]	∞	Dihedral: parallel reflections. Abstract infinite dihedral group Dih_∞.
Hyperbolic
Z_∞			[πi/λ]⁺	∞	pseudogonal group
Dih_∞			[πi/λ]	∞	full pseudogonal group

Rank three groups

Further information: Point groups in three dimensions

Finite family correspondence

Affine isomorphism and correspondences

Further information: List of spherical symmetry groups and List of planar symmetry groups

In three dimensions, the full orthorhombic group [2,2], abtractly Z₂×D₂, order 8, represents three orthogonal mirrors, (also represented by Coxeter diagram as three separate dots ). It can also can be represented as a direct product [ ]×[ ]×[ ], but the [2,2] expression allows subgroups to be defined:

First there is a "semidirect" subgroup, the orthorhombic group, [2,2⁺] (), abstractly D₁×Z₂=Z₂×Z₂, of order 4. When the + superscript is given inside of the brackets, it means reflections generated only from the adjacent mirrors (as defined by the Coxeter diagram, ) are alternated. In general, the branch orders neighboring the + node must be even. In this case [2,2⁺] and [2⁺,2] represent two isomorphic subgroups that are geometrically distinct. The other subgroups are the pararhombic group [2,2]⁺ (), also order 4, and finally the central group [2⁺,2⁺] () of order 2.

Next there is the full ortho-p-gonal group, [2,p] (), abstractly D₁×D_p=Z₂×D_p, of order 4p, representing two mirrors at a dihedral angle π/p, and both are orthogonal to a third mirror. It is also represented by Coxeter diagram as .

The direct subgroup is called the para-p-gonal group, [2,p]⁺ (), abstractly D_p, of order 2p, and another subgroup is [2,p⁺] () abstractly Z₂×Z_p, also of order 2p.

The full gyro-p-gonal group, [2⁺,2p] (), abstractly D_2p, of order 4p. The gyro-p-gonal group, [2⁺,2p⁺] (), abstractly Z_2p, of order 2p is a subgroup of both [2⁺,2p] and [2,2p⁺].

The polyhedral groups are based on the symmetry of platonic solids, the tetrahedron, octahedron, cube, icosahedron, and dodecahedron, with Schläfli symbols {3,3}, {3,4}, {4,3}, {3,5}, and {5,3} respectively. The Coxeter groups for these are called in Coxeter's bracket notation [3,3], [3,4], [3,5] called full tetrahedral symmetry, octahedral symmetry, and icosahedral symmetry, with orders of 24, 48, and 120. The front-to-back order can be reversed in the Coxeter notation, unlike the Schläfli symbol.

The tetrahedral group, [3,3], has a doubling 3,3 which maps the first and last mirrors onto each other, and this produces the [3,4] group.

In all these symmetries, alternate reflections can be removed producing the rotational tetrahedral, octahedral, and icosahedral groups of order 12, 24, and 60. The octahedral group also has a unique subgroup called the pyritohedral symmetry group, [3⁺,4], of order 12, with a mixture of rotational and reflectional symmetry.

In the Euclidean plane there's 3 fundamental reflective groups generated by 3 mirrors, represented by Coxeter diagrams , , and , and are given Coxeter notation as [4,4], [6,3], and [(3,3,3)]. The parentheses of the last group imply the diagram cycle, and also has a shorthand notation [3^[3]].

4,4 as a doubling of the [4,4] group produced the same symmetry rotated π/4 from the original set of mirrors.

Direct subgroups of rotational symmetry are: [4,4]⁺, [6,3]⁺, and [(3,3,3)]⁺. [4⁺,4] and [6,3⁺] are semidirect subgroups.

Example rank 3 finite Coxeter groups subgroup trees
Tetrahedral symmetry	Octahedral symmetry

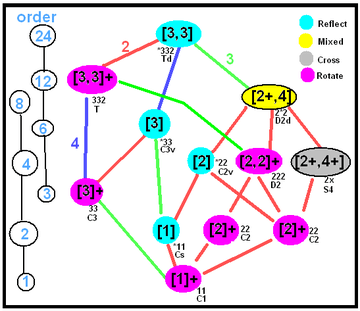Icosahedral symmetry

Finite (point groups in three dimensions)

Intl*	Geo ^[4]	Orb.	Schön.	Conway	Struct.	Coxeter		Ord.
1	1	1	C₁	C₁	Z₁	][ = [ ]⁺	=	1
2 = m	1	*	C_s	±C₁ = CD₂	D₁	[ ]		2
2 3 4 5 6 n	2 3 4 5 6 n	22 33 44 55 66 nn	C₂ C₃ C₄ C₅ C₆ C_n	C₂ C₃ C₄ C₅ C₆ C_n	Z₂ Z₃ Z₄ Z₅ Z₆ Z_n	[1,2]⁺ [1,3]⁺ [1,4]⁺ [1,5]⁺ [1,6]⁺ [1,n]⁺		2 3 4 5 6 n
2mm 3m 4mm 5m 6mm nmm nm	2 3 4 5 6 n	22 33 44 55 66 nn	C_2v C_3v C_4v C_5v C_6v C_nv	CD₄ CD₆ CD₈ CD₁₀ CD₁₂ CD_2n	D₂ D₃ D₄ D₅ D₆ D_n	[1,2] [1,3] [1,4] [1,5] [1,6] [1,n]		4 6 8 10 12 2n
2/m 3/m 4/m 5/m 6/m n/m	2 2 3 2 4 2 5 2 6 2 n 2	2* 3* 4* 5* 6* n*	C_2h C_3h C_4h C_5h C_6h C_nh	±C₂ CC₆ ±C₄ CC₁₀ ±C₆ ±C_n / CC_2n	D₁×Z₂ D₁×Z₃ D₁×Z₄ D₁×Z₅ D₁×Z₆ D₁×Z_n	[2,2⁺] [2,3⁺] [2,4⁺] [2,5⁺] [2,6⁺] [2,n⁺]		4 6 8 10 12 2n
4 3 8 5 12 2n n	2 2 1 4 2 6 2 8 2 10 2 12 2 2n 2	1× 2× 3× 4× 5× 6× n×	C_i = S₂ S₄ S₆ S₈ S₁₀ S₁₂ S_2n	CC₂ CC₄ ±C₃ CC₈ ±C₅ CC₁₂ CC_2n / ±C_n	Z₂ Z₄ Z₆=Z₂×Z₃ Z₈ Z₁₀=Z₂×Z₅ Z₁₂ Z_2n	[2⁺,2⁺] [2⁺,4⁺] [2⁺,6⁺] [2⁺,8⁺] [2⁺,10⁺] [2⁺,12⁺] [2⁺,2n⁺]		2 4 6 8 10 12 2n

Intl	Geo	Orb.	Schön.	Conway	Struct.	Coxeter	Ord.
222 32 422 52 622 n22 n2	2 2 3 2 4 2 5 2 6 2 n 2	222 223 224 225 226 22n	D₂ D₃ D₄ D₅ D₆ D_n	D₄ D₆ D₈ D₁₀ D₁₂ D_2n	D₂ D₃ D₄ D₅ D₆ D_n	[2,2]⁺ [2,3]⁺ [2,4]⁺ [2,5]⁺ [2,6]⁺ [2,n]⁺	4 6 8 10 12 2n
mmm 6m2 4/mmm 10m2 6/mmm n/mmm 2nm2	2 2 3 2 4 2 5 2 6 2 n 2	222 223 224 225 226 22n	D_2h D_3h D_4h D_5h D_6h D_nh	±D₄ DD₁₂ ±D₈ DD₂₀ ±D₁₂ ±D_2n / DD_4n	D₁×D₂ D₁×D₃ D₁×D₄ D₁×D₅ D₁×D₆ D₁×D_n	[2,2] [2,3] [2,4] [2,5] [2,6] [2,n]	8 12 16 20 24 4n
42m 3m 82m 5m 122m 2n2m nm	4 2 6 2 8 2 10 2 12 2 n 2	22 23 24 25 26 2n	D_2d D_3d D_4d D_5d D_6d D_nd	±D₄ ±D₆ DD₁₆ ±D₁₀ DD₂₄ DD_4n / ±D_2n	D₂ D₃ D₄ D₅ D₆ D_n	[2⁺,4] [2⁺,6] [2⁺,8] [2⁺,10] [2⁺,12] [2⁺,2n]	8 12 16 20 24 4n
23	3 3	332	T	T	A₄	[3,3]⁺	12
m3	4 3	3*2	T_h	±T	A₄×S₂	[3⁺,4]	24
43m	3 3	*332	T_d	TO	S₄	[3,3]	24
432	4 3	432	O	O	S₄	[3,4]⁺	24
m3m	4 3	*432	O_h	±O	S₄×S₂	[3,4]	48
532	5 3	532	I	I	A₅	[3,5]⁺	60
53m	5 3	*532	I_h	±I	A₄×S₂	[3,5]	120

Semiaffine (frieze groups)
IUC	Orb.	Geo	Sch.	Coxeter
p1	∞∞	p1	C_∞	[∞] = [∞,1]⁺ = [∞⁺,2,1⁺]	=
p1m1	*∞∞	p1	C_∞v	[∞] = [∞,1] = [∞,2,1⁺]	=
p11g	∞×	p._g1	S_2∞	[∞⁺,2⁺]
p11m	∞*	p. 1	C_∞h	[∞⁺,2]
p2	22∞	p2	D_∞	[∞,2]⁺
p2mg	2*∞	p2_g	D_∞d	[∞,2⁺]
p2mm	*22∞	p2	D_∞h	[∞,2]

Affine (Wallpaper groups)
IUC	Orb.	Geo.	Coxeter
p2	2222	p2	[4,1⁺,4]⁺
p2gg	22×	p_g2_g	[4⁺,4⁺]
p2mm	*2222	p2	[4,1⁺,4]
c2mm	2*22	c2	[[4<sup>+</sup>,4<sup>+</sup>]]
p4	442	p4	[4,4]⁺
p4gm	4*2	p_g4	[4⁺,4]
p4mm	*442	p4	[4,4]
p3	333	p3	[1⁺,6,3⁺] = [3^[3]]⁺	=
p3m1	*333	p3	[1⁺,6,3] = [3^[3]]	=
p31m	3*3	h3	[6,3⁺] = [3[3^[3]]⁺]
p6	632	p6	[6,3]⁺ = [3[3^[3]]]⁺
p6mm	*632	p6	[6,3] = [3[3^[3]]]

Subgroups

Given in Schönflies notation and Coxeter notation (orbifold notation), some low index point subgroups are:

Reflection	Reflection subgroups	Rotation subgroup	Mixed	Improper rotation	Commutator subgroup
C_1v, [1]=[ ], , (*)		C₁, [1]⁺=[ ]⁺, , (11)		S₂, [2⁺,2⁺], , (×)	[ ]⁺
C_2v, [2], , (*22)	[1⁺,2]=[1]=[ ], (*)	C₂, [2]⁺, , (22)	C_2h, [2⁺,2], , (2*)	S₄, [4⁺,2⁺], , (2×)	[ ]⁺
C_nv, [n], , (*nn)	[1⁺,2n]=[n], (*nn)	C_n, [n]⁺, , (nn)	C_nh, [n⁺,2], , (n*)	S_2n, [2n⁺,2⁺], , (n×)	[n]⁺, n odd [n/2]⁺, n even
D_nh, [2,n], , (*22n)	[1⁺,2,n]=[1,n]=[n], (*nn)	D_n, [2,n]⁺, , (22n)	D_nd, [2⁺,2n], , (2*n)		[n]⁺, n odd [n/2]⁺, n even
T_d, [3,3], , (*332)		T, [3,3]⁺, , (332)			[3,3]⁺, (332)
O_h, [4,3], , (*432)	[1⁺,4,3]=[3,3], (*332)	O, [4,3]⁺, , (432)	T_h, [3⁺,4], , (3*2)		[3,3]⁺, (332)
I_h, [5,3], , (*532)		I, [5,3]⁺, , (532)			[5,3]⁺, (532)

Given in Coxeter notation (orbifold notation), some low index affine subgroups are:

Reflective group	Reflective subgroup	Mixed subgroup	Rotation subgroup	Improper rotation/ translation	Commutator subgroup
[4,4], (*442)	[1⁺,4,4], (442) [4,1⁺,4], (2222) [1⁺,4,4,1⁺], (*2222)	[4⁺,4], (42) [(4,4,2⁺)], (222) [1⁺,4,1⁺,4], (2*22)	[4,4]⁺, (442) [1⁺,4,4⁺], (442) [1⁺,4,1⁺4,1⁺], (2222)	[4⁺,4⁺], (22×)	[4⁺,4⁺]⁺, (2222)
[6,3], (*632)	[1⁺,6,3] = [3^[3]], (*333)	[3⁺,6], (3*3)	[6,3]⁺, (632) [1⁺,6,3⁺], (333)		[1⁺,6,3⁺], (333)

Rank four groups

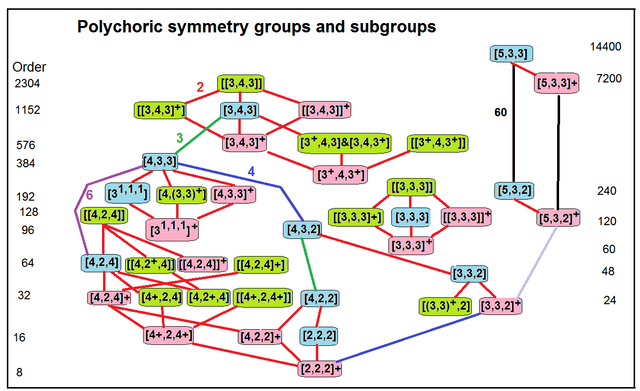Subgroup relations

Point groups

Further information: Point groups in four dimensions

Rank four groups defined the 4-dimensional point groups:

Finite groups

[ ]:
Symbol	Order
[1]⁺	1.1
[1] = [ ]	2.1

[2]:
Symbol	Order
[1⁺,2]⁺	1.1
[2]⁺	2.1
[2]	4.1

[2,2]:
Symbol	Order
[2⁺,2⁺]⁺ = [(2⁺,2⁺,2⁺)]	1.1
[2⁺,2⁺]	2.1
[2,2]⁺	4.1
[2⁺,2]	4.1
[2,2]	8.1

[2,2,2]:
Symbol	Order
[(2⁺,2⁺,2⁺,2⁺)] = [2⁺,2⁺,2⁺]⁺	1.1
[2⁺,2⁺,2⁺]	2.1
[2⁺,2,2⁺]	4.1
[(2,2)⁺,2⁺]	4
[[2⁺,2⁺,2⁺]]	4
[2,2,2]⁺	8
[2⁺,2,2]	8.1
[(2,2)⁺,2]	8
[[2⁺,2,2⁺]]	8.1
[2,2,2]	16.1
[[2,2,2]]⁺	16
[[2,2⁺,2]]	16
[[2,2,2]]	32

[p]:
Symbol	Order
[p]⁺	p
[p]	2p

[p,2]:
Symbol	Order
[p,2]⁺	2p
[p,2]	4p

[2p,2⁺]:
Symbol	Order
[2p,2⁺]	4p
[2p⁺,2⁺]	2p

[p,2,2]:
Symbol	Order
[p⁺,2,2⁺]	2p
[(p,2)⁺,2⁺]	2p
[p,2,2]⁺	4p
[p,2,2⁺]	4p
[p⁺,2,2]	4p
[(p,2)⁺,2]	4p
[p,2,2]	8p

[2p,2⁺,2]:
Symbol	Order
[2p⁺,2⁺,2⁺]	2p
[2p⁺,2⁺,2]	4p
[2p⁺,(2,2)⁺]	4p
[2p,(2,2)⁺]	8p
[2p,2⁺,2]	8p

[p,2,q]:
Symbol	Order
[p⁺,2,q⁺]	pq
[p,2,q]⁺	2pq
[p⁺,2,q]	2pq
[p,2,q]	4pq
Symbol	Order
[(p,2)⁺,2q⁺]	2pq
[(p,2)⁺,2q]	4pq

[2p,2⁺,2q]:
Symbol	Order
[2p⁺,2⁺,2q⁺]	2pq
[((2p,2)⁺,(2q,2)⁺)]	4pq
[2p,2⁺,2q⁺]	4pq
[2p,2⁺,2q]	8pq
[2p,2,2q]	16pq

[[p,2,p]]:
Symbol	Order
[[p⁺,2,p⁺]]	2p²
[[p,2,p]]⁺	4p²
[[p,2,p]⁺]	4p²
[[p,2,p]]	8p²

[[2p,2⁺,2p]]:
Symbol	Order
[[2p⁺,2⁺,2p⁺]]	4p²
[[((2p,2)⁺,(2p,2)⁺)]]	8p²
[[2p,2⁺,2p]]	16p²
[[2p,2,2p]]	32p²

[3,3,2]:
Symbol	Order
[(3,3)^Δ,2,1⁺] ≅ [2,2]⁺	4
[(3,3)^Δ,2] ≅ [2,(2,2)⁺]	8
[(3,3)^⅄,2,1⁺] ≅ [4,2⁺]	8
[(3,3)⁺,2,1⁺] = [3,3]⁺	12.5
[(3,3)^⅄,2] ≅ [2,4,2⁺]	16
[3,3,2,1⁺] = [3,3]	24
[(3,3)⁺,2]	24.10
[3,3,2]⁺	24.10
[3,3,2]	48.36

[4,3,2]:
Symbol	Order
[1⁺,4,3⁺,2,1⁺] = [3,3]⁺	12
[3⁺,4,2⁺]	24
[(3,4)⁺,2⁺]	24
[1⁺,4,3⁺,2] = [(3,3)⁺,2]	24.10
[3⁺,4,2,1⁺] = [3⁺,4]	24.10
[(4,3)⁺,2,1⁺] = [4,3]⁺	24.15
[1⁺,4,3,2,1⁺] = [3,3]	24
[1⁺,4,(3,2)⁺] = [3,3,2]⁺	24
[3,4,2⁺]	48
[4,3⁺,2]	48.22
[4,(3,2)⁺]	48
[(4,3)⁺,2]	48.36
[1⁺,4,3,2] = [3,3,2]	48.36
[4,3,2,1⁺] = [4,3]	48.36
[4,3,2]⁺	48.36
[4,3,2]	96.5

[5,3,2]:
Symbol	Order
[(5,3)⁺,2,1⁺] = [5,3]⁺	60.13
[5,3,2,1⁺] = [5,3]	120.2
[(5,3)⁺,2]	120.2
[5,3,2]⁺	120.2
[5,3,2]	240 (nc)

[3^1,1,1]:
Symbol	Order
[3^1,1,1]^Δ ≅[[4,2<sup>+</sup>,4]]⁺	32
[3^1,1,1]^⅄	64
[3^1,1,1]⁺	96.1
[3^1,1,1]	192.2
<[3,3^1,1]> = [4,3,3]	384.1
[3[3^1,1,1]] = [3,4,3]	1152.1

[3,3,3]:
Symbol	Order
[3,3,3]⁺	60.13
[3,3,3]	120.1
[[3,3,3]]⁺	120.2
[[3,3,3]⁺]	120.1
[[3,3,3]]	240.1

[4,3,3]:
Symbol	Order
[1⁺,4,(3,3)^Δ] = [3^1,1,1]^Δ ≅[[4,2<sup>+</sup>,4]]⁺	32
[4,(3,3)^Δ] = [2⁺,4[2,2,2]⁺] ≅[[4,2<sup>+</sup>,4]]	64
[1⁺,4,(3,3)^⅄] = [3^1,1,1]^⅄	64
[1⁺,4,(3,3)⁺] = [3^1,1,1]⁺	96.1
[4,(3,3)^⅄] ≅ [[4,2,4]]	128
[1⁺,4,3,3] = [3^1,1,1]	192.2
[4,(3,3)⁺]	192.1
[4,3,3]⁺	192.3
[4,3,3]	384.1

[3,4,3]:
Symbol	Order
[3⁺,4,3⁺]	288.1
[3,4,3]⁺	576.2
[3⁺,4,3]	576.1
[[3⁺,4,3⁺]]	576 (nc)
[3,4,3]	1152.1
[[3,4,3]]⁺	1152 (nc)
[[3,4,3]⁺]	1152 (nc)
[[3,4,3]]	2304 (nc)

[5,3,3]:
Symbol	Order
[5,3,3]⁺	7200 (nc)
[5,3,3]	14400 (nc)

Subgroups

1D-4D reflective point groups and subgroups
Order	Reflection	Semidirect subgroups			Direct subgroups	Commutator subgroup
2	[ ]				[ ]⁺	[ ]⁺¹	[ ]⁺
4	[2]				[2]⁺	[2]⁺²
8	[2,2]	[2⁺,2]	[2⁺,2⁺]		[2,2]⁺	[2,2]⁺³
16	[2,2,2]	[2⁺,2,2] [(2,2)⁺,2]	[2⁺,2⁺,2] [(2,2)⁺,2⁺] [2⁺,2⁺,2⁺]		[2,2,2]⁺ [2⁺,2,2⁺]	[2,2,2]⁺⁴
16	[2^1,1,1]		[(2⁺)^1,1,1]			[2,2,2]⁺⁴
2n	[n]				[n]⁺	[n]⁺¹	[n]⁺
4n	[2n]				[2n]⁺	[2n]⁺²
4n	[2,n]	[2,n⁺]			[2,n]⁺	[2,n]⁺²
8n	[2,2n]	[2⁺,2n]	[2⁺,2n⁺]		[2,2n]⁺	[2,2n]⁺³
8n	[2,2,n]	[2⁺,2,n] [2,2,n⁺]	[2⁺,(2,n)⁺]		[2,2,n]⁺ [2⁺,2,n⁺]	[2,2,n]⁺³
16n	[2,2,2n]	[2,2⁺,2n]	[2⁺,2⁺,2n] [2,2⁺,2n⁺] [(2,2)⁺,2n⁺] [2⁺,2⁺,2n⁺]		[2,2,2n]⁺ [2⁺,2n,2⁺]	[2,2,2n]⁺⁴
	[2,2n,2]		[2⁺,2n⁺,2⁺]
	[2n,2^1,1]		[2n⁺,(2⁺)^1,1]
24	[3,3]				[3,3]⁺	[3,3]⁺¹	[3,3]⁺
48	[3,3,2]	[(3,3)⁺,2]			[3,3,2]⁺	[3,3,2]⁺²
48	[4,3]	[4,3⁺]			[4,3]⁺	[4,3]⁺²
96	[4,3,2]	[(4,3)⁺,2] [4,(3,2)⁺]			[4,3,2]⁺	[4,3,2]⁺³
96	[3,4,2]	[3,4,2⁺] [3⁺,4,2]	[(3,4)⁺,2⁺]		[3⁺,4,2⁺]	[4,3,2]⁺³
120	[5,3]				[5,3]⁺	[5,3]⁺¹	[5,3]⁺
240	[5,3,2]	[(5,3)⁺,2]			[5,3,2]⁺	[5,3,2]⁺²	[5,3]⁺
4pq	[p,2,q]	[p⁺,2,q]			[p,2,q]⁺ [p⁺,2,q⁺]	[p,2,q]⁺²	[p⁺,2,q⁺]
8pq	[2p,2,q]	[2p,(2,q)⁺]	[2p⁺,(2,q)⁺]		[2p,2,q]⁺	[2p,2,q]⁺³
16pq	[2p,2,2q]	[2p,2⁺,2q]	[2p⁺,2⁺,2q] [2p⁺,2⁺,2q⁺] [(2p,(2,2q)⁺,2⁺)]	-	[2p,2,2q]⁺	[2p,2,2q]⁺⁴
120	[3,3,3]				[3,3,3]⁺	[3,3,3]⁺¹	[3,3,3]⁺
192	[3^1,1,1]				[3^1,1,1]⁺	[3^1,1,1]⁺¹	[3^1,1,1]⁺
384	[4,3,3]	[4,(3,3)⁺]			[4,3,3]⁺	[4,3,3]⁺²	[3^1,1,1]⁺
1152	[3,4,3]	[3⁺,4,3]			[3,4,3]⁺ [3⁺,4,3⁺]	[3,4,3]⁺²	[3⁺,4,3⁺]
14400	[5,3,3]				[5,3,3]⁺	[5,3,3]⁺¹	[5,3,3]⁺

Space groups

Space groups
Affine isomorphism and correspondences	8 cubic space groups as extended symmetry from [3^[4]], with square Coxeter diagrams and reflective fundamental domains	35 cubic space groups in International, Fibrifold notation, and Coxeter notation

Rank four groups as 3-dimensional space groups

Triclinic (1-2)
Coxeter	Space group
[∞⁺,2,∞⁺,2,∞⁺]	(1) P1

Monoclinic (3-15)
Coxeter	Space group
[(∞,2,∞)⁺,2,∞⁺]	(3) P2
[∞⁺,2,∞⁺,2,∞]	(6) Pm
[(∞,2,∞)⁺,2,∞]	(10) P2/m

Orthorhombic (16-74)
Coxeter	Space group
[∞,2,∞,2,∞]⁺	(16) P222
[[∞,2,∞,2,∞]]⁺	(23) I222
[∞⁺,2,∞,2,∞]	(25) Pmm2
[∞,2,∞,2,∞]	(47) Pmmm
[[∞,2,∞,2,∞]]	(71) Immm
[∞⁺,2,∞⁺,2,∞⁺]
[∞,2,∞,2⁺,∞]
[∞,2⁺,∞,2⁺,∞]

Tetragonal (75-142)
Coxeter	Space group
[(4,4)⁺,2,∞⁺]	(75) P4
[2⁺[(4,4)⁺,2,∞⁺]]	(79) I4
[(4,4)⁺,2,∞]	(83) P4/m
[2⁺[(4,4)⁺,2,∞]]	(87) I4/m
[4,4,2,∞]⁺	(89) P422
[2⁺[4,4,2,∞]]⁺	(97) I422
[4,4,2,∞⁺]	(99) P4mm
[4,4,2,∞]	(123) P4/mmm
[2⁺[4,4,2,∞]]	(139) I4/mmm
[4,(4,2)⁺,∞]	(140) I4/mcm
[4,4,2⁺,∞]
[(4,4)⁺,2⁺,∞]
[4,4,2⁺,∞⁺]
[(4,4)⁺,2⁺,∞⁺]
[4⁺,4⁺,2⁺,∞]
[4,4⁺,2,∞]
[4,4⁺,2⁺,∞]
[((4,2⁺,4)),2,∞]
[4,4⁺,2,∞⁺]
[4,4⁺,2⁺,∞⁺]
[((4,2⁺,4)),2,∞⁺]

Trigonal (143-167), rhombohedral
Coxeter	Space group

Hexagonal (168-194)
[(6,3)⁺,2,∞⁺]	(168) P6
[(6,3)⁺,2,∞]	(175) P6/m
[6,3,2,∞]⁺	(177) P622
[6,3,2,∞⁺]	(183) P6mm
[6,3,2,∞]	(191) P6/mmm
[(3^[3])⁺,2,∞⁺]
[3^[3],2,∞]
[6,3⁺,2,∞]
[6,3⁺,2,∞⁺]
[3^[3],2,∞]⁺
[3^[3],2,∞⁺]
[(3^[3])⁺,2,∞]

Cubic (195-230)
Group	Coxeter	Space group	Index
[[4,3,4]]	[[4,3,4]]	(229) Im3m	1
	[[4,3,4]]⁺	(211) I432	2
	[[4,3,4]⁺]	(223) Pm3n	2
	[[4,3⁺,4]]	(204) I3	2
	[[(4,3,4,2⁺)]]	(217) I43m	2
	[[4,3⁺,4]]⁺	(197) I23	4
	[[4,3,4]⁺]⁺	(208) P4₂32	4
	[[4,3⁺,4)]⁺]	(201) Pn43	4
	[[(4,3,4,2⁺)]⁺]	(218) P43n	4
[4,3,4]	[4,3,4]	(221) Pm3m	2
	[4,3,4]⁺	(207) P432	4
	[4,3⁺,4]	(200) Pm3	4
	[4,(3,4)⁺]	(226) Fm3c	4
	[(4,3,4,2⁺)]	(215) P43m	4
	[[{4,(3}⁺,4)⁺]]	(228) Fd3c	4
	[4,3⁺,4]⁺	(195) P23	8
	[{4,(3}⁺,4)⁺]	(219) F43c	8
[4,3^1,1]	[4,3^1,1]	(225) Fm3m	4
	[4,(3^1,1)⁺]	(202) Fm3	8
	[4,3^1,1]⁺	(209) F432	8
[[3^[4]]]
	[(4⁺,2⁺)[3^[4]]]	(222) Pn3n	2
	[[3^[4]]]	(227) Fd3m	4
	[[3^[4]]]⁺	(203) Fd3	8
	[[3^[4]]⁺]	(210) F4₁32	8
[3^[4]]	[3^[4]]	(216) F43m	8
[3^[4]]	[3^[4]]⁺	(196) F23	16

Line groups

Rank four groups also defined the 3-dimensional line groups:

Semiaffine (3D) groups
Point group			Line group
Hermann-Mauguin		Schönflies	Hermann-Mauguin		Offset type	Wallpaper			Coxeter [∞_h,2,p_v]
Even n	Odd n	Schönflies	Even n	Odd n	Offset type	IUC	Orbifold	Diagram	Coxeter [∞_h,2,p_v]
n		C_n	Pn_q		Helical: q	p1	o		[∞⁺,2,n⁺]
2n	n	S_2n	P2n	Pn	None	p11g, pg(h)	××		[(∞,2)⁺,2n⁺]
n/m	2n	C_nh	Pn/m	P2n	None	p11m, pm(h)	**		[∞⁺,2,n]
2n/m		C_2nh	P2n_n/m		Zigzag	c11m, cm(h)	*×		[∞⁺,2⁺,2n]
nmm	nm	C_nv	Pnmm	Pnm	None	p1m1, pm(v)	**		[∞,2,n⁺]
nmm	nm	C_nv	Pncc	Pnc	Planar reflection	p1g1, pg(v)	××		[∞⁺,(2,n)⁺]
2nmm		C_2nv	P2n_nmc		Zigzag	c1m1, cm(v)	*×		[∞,2⁺,2n⁺]
n22	n2	D_n	Pn_q22	Pn_q2	Helical: q	p2	2222		[∞,2,n]⁺
2n2m	nm	D_nd	P2n2m	Pnm	None	p2mg, pmg(h)	22*		[(∞,2)⁺,2n]
2n2m	nm	D_nd	P2n2c	Pnc	Planar reflection	p2gg, pgg	22×		[⁺(∞,(2),2n)⁺]
n/mmm	2n2m	D_nh	Pn/mmm	P2n2m	None	p2mm, pmm	*2222		[∞,2,n]
n/mmm	2n2m	D_nh	Pn/mcc	P2n2c	Planar reflection	p2mg, pmg(v)	22*		[∞,(2,n)⁺]
2n/mmm		D_2nh	P2n_n/mcm		Zigzag	c2mm, cmm	2*22		[∞,2⁺,2n]

Duoprismatic group

Extended duoprismatic symmetry

Extended duoprismatic groups, [p]×[p] or [p,2,p] or , expressed in relation to its tetragonal disphenoid fundamental domain symmetry.

Rank four groups defined the 4-dimensional duoprismatic groups. In the limit as p and q go to infinity, they degenerate into 2 dimensions and the wallpaper groups.

Duoprismatic groups (4D)
Wallpaper			Coxeter [p,2,q]	Coxeter p,2,p	Wallpaper
IUC	Orbifold	Diagram	Coxeter [p,2,q]	Coxeter p,2,p	IUC	Orbifold	Diagram
p1	o		[p⁺,2,q⁺]	[[p<sup>+</sup>,2,p<sup>+</sup>]]	p1	o
pg	××		[(p,2)⁺,2q⁺]	-
pm	**		[p⁺,2,q]	-
cm	*×		[2p⁺,2⁺,2q]	-
p2	2222		[p,2,q]⁺	p,2,p⁺	p4	442
pmg	22*		[(p,2)⁺,2q]	-
pgg	22×		[⁺(2p,(2),2q)⁺]	[[<sup>+</sup>(2p,(2),2p)<sup>+</sup>]]	cmm	2*22
pmm	*2222		[p,2,q]	p,2,p	p4m	*442
cmm	2*22		[2p,2⁺,2q]	[[2p,2<sup>+</sup>,2p]]	p4g	4*2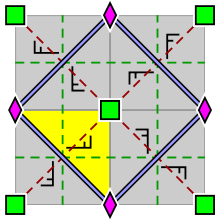

Wallpaper groups

Rank four groups also defined some of the 2-dimensional wallpaper groups, as limiting cases of the four-dimensional duoprism groups:

Affine (2D plane)

IUC	Orb.	Geo	Coxeter
p1	o	p1	[∞⁺,2,∞⁺]
			[∞⁺,2⁺,∞⁺]
			[(∞⁺,2⁺,∞⁺,2⁺)]
p2	2222	p2	[∞,2,∞]⁺
p2	2222	p2	[(∞,2⁺,∞,2⁺)]
p11g	××	p_g1	h: [∞⁺,(2,∞)⁺]
p1g1	××	p_g1	v: [(∞,2)⁺,∞⁺]
p2gm	22*	p_g2	h: [(∞,2)⁺,∞]
p2mg	22*	p_g2	v: [∞,(2,∞)⁺]

IUC	Orb.	Geo	Coxeter
p11m	**	p1	h: [∞⁺,2,∞]
p1m1	**	p1	v: [∞,2,∞⁺]
p2mm	*2222	p2	[∞,2,∞]
c11m	*×	c1	h: [∞⁺,2⁺,∞]
c1m1	*×	c1	v: [∞,2⁺,∞⁺]
p2gg	22×	p_g2_g	[⁺(∞,(2),∞)⁺] [((∞,2)⁺)^[2]]
c2mm	2*22	c2	[∞,2⁺,∞]

Subgroups of [∞,2,∞], (*2222) can be expressed down to its index 16 commutator subgroup:

Subgroups of [∞,2,∞]
Reflective group	Reflective subgroup	Mixed subgroup	Rotation subgroup	Improper rotation/ translation	Commutator subgroup
[∞,2,∞], (*2222)	[1⁺,∞,2,∞], (*2222)	[∞⁺,2,∞], (**)	[∞,2,∞]⁺, (2222)	[∞,2⁺,∞]⁺, (°) [∞⁺,2⁺,∞⁺], (°) [∞⁺,2,∞⁺], (°) [∞⁺,2⁺,∞], (*×) [(∞,2)⁺,∞⁺], (××) [⁺(∞,(2),∞)⁺], (22×)	[(∞⁺,2⁺,∞⁺,2⁺)], (°)
[∞,2,∞], (*2222)	[1⁺,∞,2,∞], (*2222)	[∞,2⁺,∞], (222) [(∞,2)⁺,∞], (22)	[∞,2,∞]⁺, (2222)		[(∞⁺,2⁺,∞⁺,2⁺)], (°)

Complex reflections

All subgroup relations on rank 2 Shephard groups.

Coxeter notation has been extended to Complex space, Cⁿ where nodes are unitary reflections of period greater than 2. Nodes are labeled by an index, assumed to be 2 for ordinary real reflection if suppressed. Complex reflection groups are called Shephard groups rather than Coxeter groups, and can be used to construct complex polytopes.

In $\mathbb{C}^1$ , a rank 1 shephard group , order p, is represented as _p[], []_p or ]_p[. It has a single generator, representing a 2π/p radian rotation in the Complex plane: $e^{2\pi i/p}$ .

Coxeter writes the rank 2 complex group, _p[q]_r represents Coxeter diagram . The p and r should only be suppressed if both are 2, which is the real case [q]. The order of a rank 2 group _p[q]_r is $g=8/q(1/p+2/q+1/r-1)^{-2}$ .^[5]

The rank 2 solutions that generate complex polygons are: _p[4]₂ (p is 2,3,4,...), ₃[3]₃, ₃[6]₂, ₃[4]₃, ₄[3]₄, ₃[8]₂, ₄[6]₂, ₄[4]₃, ₃[5]₃, ₅[3]₅, ₃[10]₂, ₅[6]₂, and ₅[4]₃ with Coxeter diagrams , , , , , , , , , , , , .

Some subgroup relations among infinite Shephard groups

Infinite groups are ₃[12]₂, ₄[8]₂, ₆[6]₂, ₃[6]₃, ₆[4]₃, ₄[4]₄, and ₆[3]₆ or , , , , , , .

Index 2 subgroups exists by removing a real reflection: _p[2q]₂ → _p[q]_p. Also index r subgroups exist for 4 branches: _p[4]_r → _p[r]_p.

For the infinite family _p[4]₂, for any p = 2, 3, 4,..., there are two subgroups: _p[4]₂ → [p], index p, while and _p[4]₂ → _p[]×_p[], index 2.

Notes

↑ Conway, 2003, p.46, Table 4.2 Chiral groups II
↑ Coxeter and Moser, 1980, Sec 9.5 Commutator subgroup, p. 124–126
↑ Norman W. Johnson, Asia Ivić Weiss, Quaternionic modular groups, Linear Algebra and its Applications, Volume 295, Issues 1–3, 1 July 1999, Pages 159–189
↑ The Crystallographic Space groups in Geometric algebra, D. Hestenes and J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 pages) PDF
↑ Coxeter, Regular Complex Polytopes, 9.7 Two-generator subgroups reflections. pp. 178–179

References

H.S.M. Coxeter:
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  - (Paper 22) Coxeter, H.S.M. (1940), "Regular and Semi Regular Polytopes I", Math. Zeit., 46: 380–407
  - (Paper 23) Coxeter, H.S.M. (1985), "Regular and Semi-Regular Polytopes II", Math. Zeit., 188: 559–591
  - (Paper 24) Coxeter, H.S.M. (1988), "Regular and Semi-Regular Polytopes III", Math. Zeit., 200: 3–45
Coxeter, H. S. M.; Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Norman W. Johnson and Asia Ivic Weiss Quadratic Integers and Coxeter Groups PDF Canad. J. Math. Vol. 51 (6), 1999 pp. 1307–1336
- N. W. Johnson: Geometries and Transformations, (2017) ISBN 9781107103405 Chapter 11: Finite symmetry groups
Conway, John Horton; Delgado Friedrichs, Olaf; Huson, Daniel H.; Thurston, William P. (2001), "On three-dimensional space groups", Beiträge zur Algebra und Geometrie. Contributions to Algebra and Geometry, 42 (2): 475–507, ISSN 0138-4821, MR 1865535
John H. Conway and Derek A. Smith, On Quaternions and Octonions, 2003, ISBN 978-1-56881-134-5
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 Ch.22 35 prime space groups, ch.25 184 composite space groups, ch.26 Higher still, 4D point groups

This article is issued from Wikipedia - version of the 10/31/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.