Decomino
A decomino, or 10-omino, is a polyomino of order 10, that is, a polygon in the plane made of 10 equal-sized squares connected edge-to-edge.[1] When rotations and reflections are not considered to be distinct shapes, there are 4,655 different free decominoes (the free decominoes comprise 195 with holes and 4,460 without holes). When reflections are considered distinct, there are 9,189 one-sided decominoes. When rotations are also considered distinct, there are 36,446 fixed decominoes.[2]
Symmetry
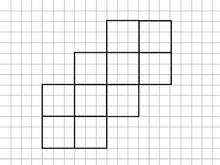
The 4,655 free decominoes can be classified according to their symmetry groups:[2]
- 4,461 decominoes have no symmetry. Their symmetry group consists only of the identity mapping.
- 90 decominoes have an axis of reflection symmetry aligned with the gridlines. Their symmetry group has two elements, the identity and the reflection in a line parallel to the sides of the squares.
- 22 decominoes have an axis of reflection symmetry at 45° to the gridlines. Their symmetry group has two elements, the identity and a diagonal reflection.
- 73 decominoes have point symmetry, also known as rotational symmetry of order 2. Their symmetry group has two elements, the identity and the 180° rotation.
- 8 decominoes have two axes of reflection symmetry, both aligned with the gridlines. Their symmetry group has four elements, the identity, two reflections and the 180° rotation. It is the dihedral group of order 2, also known as the Klein four-group.
- 1 decomino has two axes of reflection symmetry, both aligned with the diagonals. Its symmetry group is also the dihedral group of order 2 with four elements.
Unlike both octominoes and nonominoes, no decomino has rotational symmetry of order 4.
Packing and tiling
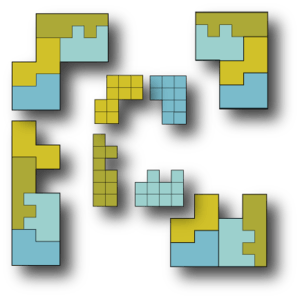
195 decominoes have holes. This makes it trivial to prove that the complete set of decominoes cannot be packed into a rectangle, and that not all decominoes can be tiled.
The 4,460 decominos without holes comprise 44,600 unit squares. Thus, the largest square that can be tiled with distinct decominoes is at most 210 units on a side (210 squared is 44,100). Such a square containing 4,410 decominoes was constructed by Livio Zucca.[3]
References
- ↑ Golomb, Solomon W. (1994). Polyominoes (2nd ed.). Princeton, New Jersey: Princeton University Press. ISBN 0-691-02444-8.
- 1 2 Redelmeier, D. Hugh (1981). "Counting polyominoes: yet another attack". Discrete Mathematics. 36 (2): 191–203. doi:10.1016/0012-365X(81)90237-5.
- ↑ Iread.it: Maximal squares of polyominoes