GOST (block cipher)

GOST 28147-89 (Magma)
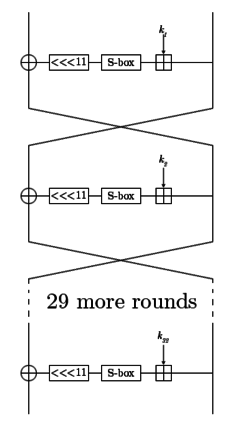Diagram of GOST
General
Designers USSR, KGB, 8th Department
First published 1994-05-23 (declassified)
Successors GOST hash function, Kuznyechik
Certification GOST standard
Cipher detail
Key sizes 256 bits
Block sizes 64 bits
Structure Feistel network
Rounds 32

The GOST block cipher, defined in the standard GOST 28147-89, is a Soviet and Russian government standard symmetric key block cipher. The original standard did not give the cipher any name, however, the most recent revision of the standard, GOST R 34.12-2015, specifies that it may be referred to as Magma.[1] Also based on this block cipher is the GOST hash function.

Developed in the 1970s, the standard had been marked "Top Secret" and then downgraded to "Secret" in 1990. Shortly after the dissolution of the USSR, it was declassified and it was released to the public in 1994. GOST 28147 was a Soviet alternative to the United States standard algorithm, DES.[2] Thus, the two are very similar in structure.

The algorithm

GOST has a 64-bit block size and a key length of 256 bits. Its S-boxes can be secret, and they contain about 354 (log2(16!8)) bits of secret information, so the effective key size can be increased to 610 bits; however, a chosen-key attack can recover the contents of the S-Boxes in approximately 232 encryptions.[3]

GOST is a Feistel network of 32 rounds. Its round function is very simple: add a 32-bit subkey modulo 232, put the result through a layer of S-boxes, and rotate that result left by 11 bits. The result of that is the output of the round function. In the adjacent diagram, one line represents 32 bits.

The subkeys are chosen in a pre-specified order. The key schedule is very simple: break the 256-bit key into eight 32-bit subkeys, and each subkey is used four times in the algorithm; the first 24 rounds use the key words in order, the last 8 rounds use them in reverse order.

The S-boxes accept a four-bit input and produce a four-bit output. The S-box substitution in the round function consists of eight 4 × 4 S-boxes. The S-boxes are implementation-dependent – parties that want to secure their communications using GOST must be using the same S-boxes. For extra security, the S-boxes can be kept secret. In the original standard where GOST was specified, no S-boxes were given, but they were to be supplied somehow. This led to speculation that organizations the government wished to spy on were given weak S-boxes. One GOST chip manufacturer reported that he generated S-boxes himself using a pseudorandom number generator.[4]

For example, the Central Bank of Russian Federation uses the following S-boxes:

# S-Box
1 4 10 9 2 13 8 0 14 6 11 1 12 7 15 5 3
2 14 11 4 12 6 13 15 10 2 3 8 1 0 7 5 9
3 5 8 1 13 10 3 4 2 14 15 12 7 6 0 9 11
4 7 13 10 1 0 8 9 15 14 4 6 12 11 2 5 3
5 6 12 7 1 5 15 13 8 4 10 9 14 0 3 11 2
6 4 11 10 0 7 2 1 13 3 6 8 5 9 12 15 14
7 13 11 4 1 3 15 5 9 0 10 14 7 6 8 2 12
8 1 15 13 0 5 7 10 4 9 2 3 14 6 11 8 12

However, the most recent revision of the standard, GOST R 34.12-2015, adds the missing S-Box specification and defines it as follows.[1]

# GOST R 34.12-2015 S-Box
1 C 4 6 2 A 5 B 9 E 8 D 7 0 3 F 1
2 6 8 2 3 9 A 5 C 1 E 4 7 B D 0 F
3 B 3 5 8 2 F A D E 1 7 4 C 9 6 0
4 C 8 2 1 D 4 F 6 7 0 A 5 3 E 9 B
5 7 F 5 A 8 1 6 D 0 9 3 E B 4 2 C
6 5 D F 6 9 2 C A B 7 8 1 4 3 E 0
7 8 E 2 5 6 9 1 C F 4 B 0 D A 3 7
8 1 7 E D 0 5 8 3 4 F A 6 9 C B 2

Cryptanalysis of GOST

Compared to DES, GOST has a very simple round function. However, the designers of GOST attempted to offset the simplicity of the round function by specifying the algorithm with 32 rounds and secret S-boxes.

Another concern is that the avalanche effect is slower to occur in GOST than in DES. This is because of GOST's lack of an expansion permutation in the round function, as well as its use of a rotation instead of a permutation. Again, this is offset by GOST's increased number of rounds.

There is not much published cryptanalysis of GOST, but a cursory glance says that it seems secure.[4][5] The large number of rounds and secret S-boxes makes both linear and differential cryptanalysis difficult. Its avalanche effect may be slower to occur, but it can propagate over 32 rounds very effectively.

However, GOST is not fully defined by its standard: It does not specify the S-boxes (replacement tables). On the one hand, this can be additional secure information (in addition to key). On the other hand, the following problems arise:

Despite its apparently strong construction, GOST is vulnerable to generic attacks based on its short (64-bit) block size, and should therefore never be used in contexts where more than 232 blocks could be encrypted with the same key.

Since 2007, several attacks were developed against GOST implementations with reduced number of rounds and/or keys with additional special properties.[6][7]

In 2011 several authors discovered more significant flaws in GOST cipher, being able to attack full 32-round GOST with arbitrary keys for the first time. It has been even called "a deeply flawed cipher" by Nicolas Courtois.[8] First attacks were able to reduce time complexity from 2256 to 2228 at the cost of huge memory requirements,[9] and soon they were improved up to 2178 time complexity (at the cost of 270 memory and 264 data).[10]

As of December 2012 the best known attack on GOST can find a key by computing only 2101 GOST rounds.[11]

GOST has been submitted to be included in ISO-18033 in 2010.

See also

References

  1. 1 2 GOST R 34.12-2015 (Russian only)
  2. ↑ Fleischmann, Ewan; Gorski, Michael; Hühne, Jan-Hendrik; Lucks, Stefan (2009). "Key Recovery Attack on Full GOST Block Cipher with Zero Time and Memory". Published as ISO/IEC JTC. 1.
  3. ↑ Saarinen, Markku-Juhani (1998). "A chosen key attack against the secret S-boxes of GOST". We show that a simple "black box" chosen-key attack against GOST can recover secret S-boxes with approximately 2^32 encryptions
  4. 1 2 Schneier, Bruce (1996). Applied cryptography : protocols, algorithms, and source code in C (2. ed., [Nachdr.] ed.). New York [u.a.]: Wiley. ISBN 0-471-11709-9.
  5. ↑ Shorin, Vitaly V.; Jelezniakov, Vadim V.; Gabidulin, Ernst M. (April 2001). "Linear and Differential Cryptanalysis of Russian GOST". Electronic Notes in Discrete Mathematics. 6: 538–547. doi:10.1016/S1571-0653(04)00206-9. In this paper the linear cryptanalysis and the differential cryptanalysis of the Russian GOST encryption algorithm are carried out [2]. It is shown that GOST is secure against the linear cryptanalysis after five rounds and against the differential cryptanalysis after seven rounds. The differential analysis algorithm of the three round GOST is given. Also criteria for selection of the substitution boxes with provable security against linear cryptanalysis are given.
  6. ↑ Eli Biham; Orr Dunkelman; Nathan Keller (2007). "Improved Slide Attacks" (PDF).
  7. ↑ Orhun Kara (2008). "Reflection Cryptanalysis of Some Ciphers".
  8. ↑ Courtois, Nicolas T. (9 May 2011). "Security Evaluation of GOST 28147-89 In View Of International Standardisation". Cryptology ePrint Archive. IACR. Until 2011 researchers unanimously agreed that GOST could or should be very secure, which was summarized in 2010 in these words: despite considerable cryptanalytic efforts spent in the past 20 years, GOST is still not broken". Unhappily, it was recently discovered that GOST can be broken and is a deeply flawed cipher
  9. ↑ Nicolas T. Courtois; Michał Miształ (2011). "Differential Cryptanalysis of GOST". IACR.
  10. ↑ Nicolas T. Courtois (2012). "An Improved Differential Attack on Full GOST" (PDF). IACR.
  11. ↑ Nicolas T. Courtois; Jerzy A. Gawinecki; Guangyan Song (2012). "CONTRADICTION IMMUNITY AND GUESS-THEN-DETERMINE ATTACKS ON GOST" (PDF). Versita. Retrieved 2014-08-25.

Further reading

External links

This article is issued from Wikipedia - version of the 11/22/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.