Goldberg polyhedron
 G(1,4) |
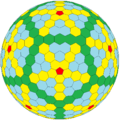 G(4,4) |
 G(7,0) |
 G(5,3) |
A Goldberg polyhedron is a convex polyhedron made from hexagons and pentagons. They were first described by Michael Goldberg (1902–1990) in 1937. They are defined by three properties: each face is either a pentagon or hexagon, exactly three faces meet at each vertex, they have rotational icosahedral symmetry. They are not necessarily mirror-symmetric; e.g. G(5,3) and G(3,5) are enantiomorphs of each other. A consequence of Euler's polyhedron formula is that there will be exactly twelve pentagons.
Icosahedral symmetry ensures that the pentagons are always regular, although many of the hexagons may not be. Typically all of the vertices lie on a sphere.
It is a dual polyhedron of a geodesic sphere, with all triangle faces and 6 triangles per vertex, except for 12 vertices with 5 triangles.
Simple examples of Goldberg polyhedra include the dodecahedron and truncated icosahedron. Other forms can be described by taking a chess knight move from one pentagon to the next: first take m steps in one direction, then turn 60° to the left and take n steps. Such a polyhedron is denoted G(m,n). A dodecahedron is G(1,0) and a truncated icosahedron is G(1,1).
A similar technique can be applied to construct polyhedra with tetrahedral symmetry and octahedral symmetry. These polyhedra will have triangles or squares rather than pentagons. These variations are given Roman numeral subscripts: GIII(n,m), GIV(n,m), and GV(n,m).
Polyhedral elements
The number of vertices, edges, and faces of G(m,n) can be computed from m and n, with T = m2 + mn + n2 = (m + n)2 − mn, depending on one of three symmetry systems:[1]
| System | Vertices | Edges | Faces | Faces by type |
|---|---|---|---|---|
| Tetrahedral GIII(m,n) |
4T | 6T | 2T + 2 | 4 {3} and 2(T − 1) {6} |
| Octahedral GIV(m,n) |
8T | 12T | 4T + 2 | 6 {4} and 4(T − 1) {6} |
| Icosahedral GV(m,n) |
20T | 30T | 10T + 2 | 12 {5} and 10(T − 1) {6} |
Small examples by symmetry family
A few polyhedra are given with Conway polyhedron notation starting with (T)etrahedron, (C)ube, (O)ctahedron, and (D)odecahedron, (I)cosahedron seeds. The operator dk (dual kis) generates G(1,1). The chamfer operator, c, replaces all edges by hexagons and transforms G(m,n) to G(2m,2n). In addition, the tk operator, transforms G(m,n) to G(3m,3n).
| System | G(0,1) T = 1 |
G(0,2) T = 4 |
G(0,3) T = 9 |
G(0,4) T = 16 |
G(0,5) T = 25 |
G(0,6) T = 36 |
G(0,7) T = 49 |
G(0,8) T = 64 |
G(0,9) T = 81 |
G(0,12) T = 144 |
G(0,16) T = 256 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tetrahedral GIII(0,n) |
 (T) |
 (cT) |
 (tkT) |
(ccT) | (ctkT) | (wrwT) | (cccT) |  (tktkT) |
(cctkT) | (ccccT) | |
| Octahedral GIV(0,n) |
 (C) |
 (cC) |
 (tkC) |
 (ccC) |
(ctkC) | (wrwC) |  (cccC) |
 (tktkC) |
(cctkC) | (ccccC) | |
| Icosahedral GV(0,n) |
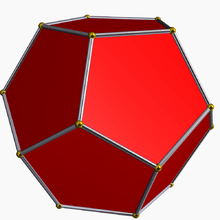 (D) |
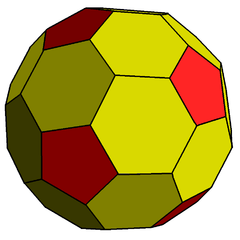 (cD) |
(tkD) |
 (ccD) |
 (ctkD) |
 (wrwD) |
 (cccD) |
 (tktkD) |
 (cctkD) |
 (ccccD) |
| System | G(1,1) T = 3 |
G(2,2) T = 12 |
G(3,3) T = 27 |
G(4,4) T = 48 |
G(6,6) T = 108 |
G(8,8) T = 192 |
G(9,9) T = 243 |
|---|---|---|---|---|---|---|---|
| Tetrahedral GIII(n,n) |
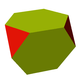 (tT) |
(ctT) |  (tktT) |
(cctT) | (ctktT) | (ccctT) | (tktktT) |
| Octahedral GIV(n,n) |
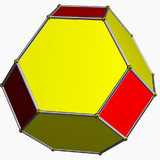 (tO) |
 (ctO) |
 (tktO) |
 (cctO) |
(ctktO) | (ccctO) | (tktktO) |
| Icosahedral GV(n,n) |
 (tI) |
 (ctI) |
 (tktI) |
 (cctI) |
(ctktI) | (ccctI) | (tktktI) |
| System | G(2,1) T = 7 |
G(3,1) T = 13 |
G(3,2) T = 19 |
G(4,1) T = 21 |
G(4,2) T = 28 |
G(4,3) T = 37 |
G(5,1) T = 31 |
G(5,2) T = 39 |
G(5,3) T = 49 |
G(5,4) T = 61 |
|---|---|---|---|---|---|---|---|---|---|---|
| Tetrahedral GIII(m,n) |
||||||||||
| Octahedral GIV(m,n) |
||||||||||
| Icosahedral GV(m,n) |
 (wD) |
 |
 |
 (tk5sD) |
 (cwD) |
 |
 |
 |
Icosahedral G(0,n) polyhedra
Goldberg polyhedra of the form G(0,n) have full icosahedral symmetry, Ih, [5,3], (*532). G(0,n) has 10(n2 − 1) hexagons.
| Index | G(0,1) | G(0,2) | G(0,3) | G(0,4) | G(0,5) | G(0,6) | |
|---|---|---|---|---|---|---|---|
| Image |  |
 |
 |
 |
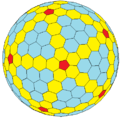 |
 | |
| Conway notation | D | cD[2] | dktI=tdtI[3] | ccD[4] | cdktI[5] | ||
| Vertices | 20 | 80 | 180 | 320 | 500 | 720 | |
| Edges | 30 | 120 | 270 | 480 | 750 | 1080 | |
| Hexagons | 0 | 30 | 80 | 150 | 240 | 350 | |
| Index | G(0,7) | G(0,8) | G(0,9) | G(0,10) | G(0,12) | G(0,16) | G(0,n) |
| Image |  |
 |
 |
 |
 |
 |
 |
| Conway notation | wrwD[6] | cccD[7] | tdtdtkD[8] | ccccD[9] | |||
| Vertices | 980 | 1280 | 1620 | 2000 | 2880 | 5120 | 20n2 |
| Edges | 1470 | 1920 | 2430 | 3000 | 4320 | 7650 | 30n2 |
| Hexagons | 480 | 630 | 800 | 990 | 1430 | 2550 | 10(n2 − 1) |
Icosahedral G(n,n) polyhedra
Goldberg polyhedra of the form G(n,n) have full icosahedral symmetry, Ih, [5,3], (*532). G(n,n) has 10(3n2 − 1) hexagons.
| Index | G(1,1) | G(2,2) | G(3,3) | G(4,4) | G(5,5) | G(6,6) | G(n,n) |
|---|---|---|---|---|---|---|---|
| Image |  |
 |
 |
 |
 | ||
| Conway notation | tI[10] | ctI[11] | tktI[12] | cctI[13] | ctktI[14] | ||
| Vertices | 60 | 240 | 540 | 960 | 1500 | 2160 | 60n2 |
| Edges | 90 | 360 | 810 | 1440 | 2250 | 3240 | 90n2 |
| Hexagons | 20 | 110 | 260 | 470 | 740 | 1070 | 10(3n2 − 1) |
Icosahedral G(m,n) polyhedra
General Goldberg polyhedra (m > 0 and n > 0) with m ≠ n have chiral (rotational) icosahedral symmetry, I, [5,3] + , (532). In such cases G(n,m) and G(m,n) are mirror images.
| Index | G(1,0) | G(1,1) | G(1,2) | G(1,3) | G(1,4) | G(1,5) | G(1,n) |
|---|---|---|---|---|---|---|---|
| Image |  |
 |
 |
 |
 |
 |
... |
| Conway notation | D | dkD[15] | wD[16] | wdkD[17] | |||
| Vertices | 20 | 60 | 140 | 260 | 420 | 620 | 20(n2 + n + 1) |
| Edges | 30 | 90 | 210 | 390 | 630 | 930 | 30(n2 + n + 1) |
| Hexagons | 0 | 20 | 60 | 120 | 200 | 300 | 10n(n + 1) |
| Index | G(2,0) | G(2,1) | G(2,2) | G(2,3) | G(2,4) | G(2,5) | G(2,n) |
|---|---|---|---|---|---|---|---|
| Image |  |
 |
 |
 |
 |
||
| Conway notation | cD[18] | dk5sD=t5gD=wD[19] | dkt5daD[20] | wcD = wcD[21] | |||
| Vertices | 80 | 140 | 240 | 380 | 560 | 20(n2 + 2n + 4) | |
| Edges | 120 | 210 | 360 | 570 | 840 | 30(n2 + 2n + 4) | |
| Hexagons | 30 | 60 | 110 | 180 | 270 | 10(n2 + 2n + 3) |
| Index | G(3,0) | G(3,1) | G(3,2) | G(3,3) | G(3,4) | G(3,5) | G(3,n) |
|---|---|---|---|---|---|---|---|
| Image |  |
 |
 |
 |
 |
 |
|
| Conway notation | tkD[22] | wwD[23] | |||||
| Vertices | 180 | 260 | 380 | 540 | 740 | 980 | 20(n2 + 3n + 9) |
| Edges | 270 | 390 | 570 | 810 | 1110 | 1470 | 30(n2 + 3n + 9) |
| Hexagons | 80 | 120 | 180 | 260 | 360 | 480 | 10(n2 + 3n + 8) |
| Index | G(4,0) | G(4,1) | G(4,2) | G(4,3) | G(4,4) | G(4,5) | G(4,6) | G(4,n) |
|---|---|---|---|---|---|---|---|---|
| Image |  |
 |
 |
 |
 |
|||
| Conway notation | ccD[24] | dkwD[25] | wcD[26] | cdkt5daD[27] | ||||
| Vertices | 320 | 420 | 560 | 740 | 960 | 1220 | 1520 | 20(n2 + 4n + 16) |
| Edges | 480 | 630 | 840 | 1110 | 1440 | 1830 | 2280 | 30(n2 + 4n + 16) |
| Hexagons | 150 | 200 | 270 | 360 | 470 | 600 | 750 | 10(n2 + 4n + 15) |
| Index | G(5,0) | G(5,1) | G(5,2) | G(5,3) | G(5,4) | G(5,5) | G(5,6) | G(5,n) |
|---|---|---|---|---|---|---|---|---|
| Image |  |
 |
 |
|||||
| Vertices | 500 | 620 | 780 | 980 | 1220 | 1500 | 1820 | 20(n2 + 5n + 25) |
| Edges | 750 | 930 | 1170 | 1470 | 1830 | 2250 | 2730 | 30(n2 + 5n + 25) |
| Hexagons | 240 | 300 | 380 | 480 | 600 | 740 | 900 | 10(n2 + 5n + 24) |
| Index | G(6,0) | G(6,1) | G(6,2) | G(6,3) | G(6,4) | G(6,5) | G(6,6) | G(6,n) |
|---|---|---|---|---|---|---|---|---|
| Image |  |
|||||||
| Conway notation | tkt5daD=ctkD[28] | |||||||
| Vertices | 720 | 860 | 1040 | 1260 | 1520 | 1820 | 2160 | 20(n2 + 6n + 36) |
| Edges | 1080 | 1290 | 1560 | 1890 | 2280 | 2730 | 3240 | 30(n2 + 6n + 36) |
| Hexagons | 350 | 420 | 510 | 620 | 750 | 900 | 1070 | 10(n2 + 6n + 35) |
See also
Notes
References
- Goldberg, Michael (1937). "A class of multi-symmetric polyhedra". Tohoku Mathematical Journal.
- Joseph D. Clinton, Clinton’s Equal Central Angle Conjecture
- Hart, George (2012). "Goldberg Polyhedra". In Senechal, Marjorie. Shaping Space (2nd ed.). Springer. pp. 125–138. doi:10.1007/978-0-387-92714-5_9.
- Hart, George (June 18, 2013). "Mathematical Impressions: Goldberg Polyhedra". Simons Science News.
- Fourth class of convex equilateral polyhedron with polyhedral symmetry related to fullerenes and viruses, Stan Schein and James Maurice Gaye, PNAS, Early Edition doi: 10.1073/pnas.1310939111
External links
- Dual Geodesic Icosahedra
- Goldberg variations: New shapes for molecular cages Flat hexagons and pentagons come together in new twist on old polyhedral, by Dana Mackenzie, February 14, 2014