Golden rhombus
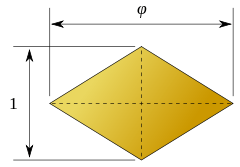
The golden rhombus.
In geometry, a golden rhombus is a rhombus whose diagonals are in the ratio , where is the golden ratio.
Element
The internal angles of the rhombus are
- degrees
- degrees, which is also the dihedral angle of the dodecahedron
The edge length of the golden rhombus with short diagonal is
A golden rhombus with unit edge length has diagonal lengths
Polyhedra
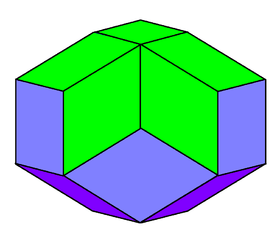
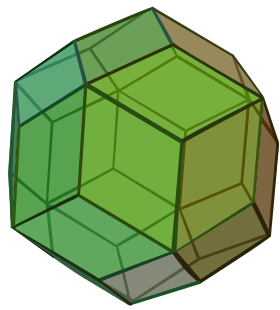
Several notable polyhedra have golden rhombi as their faces. They include the two golden rhombohedra (with six faces each), the Bilinski dodecahedron (with 12 faces), the rhombic icosahedron (with 20 faces), the rhombic triacontahedron (with 30 faces), and the nonconvex rhombic hexecontahedron (with 60 faces). The first five of these are the only convex polyhedra with golden rhomb faces, but there exist infinitely many nonconvex polyhedra having this shape for all of its faces.[1]
See also
References
- M. Livio, The Golden Ratio: The Story of Phi, the World's Most Astonishing Number, New York: Broadway Books, p. 206, 2002.
External links
This article is issued from Wikipedia - version of the 5/27/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.