Goode homolosine projection

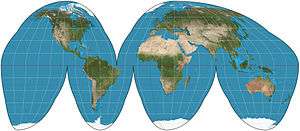
Goode homolosine projection of the world.
Tissot indicatrix on Goode homolosine projection, 15° graticule.

The Goode homolosine projection (or interrupted Goode homolosine projection) is a pseudocylindrical, equal-area, composite map projection used for world maps. Normally it is presented with multiple interruptions. Its equal-area property makes it useful for presenting spatial distribution of phenomena.

The projection was developed in 1923 by John Paul Goode to provide an alternative to the Mercator projection for portraying global areal relationships. Goode offered variations of the interruption scheme for emphasizing the world’s land masses and the world’s oceans. Some variants include extensions that repeat regions in two different lobes of the interrupted map in order to show Greenland or eastern Russia undivided. The homolosine evolved from Goode’s 1916 experiments in interrupting the Mollweide projection.

Because the Mollweide is sometimes called the "homolographic projection", Goode fused the two names "homolographic" and "sinusoidal" to create the name “homolosine”. Common in the 1960s, the Goode homolosine projection is often called an "orange-peel map" because of its resemblance to the flattened rind of a hand-peeled orange. In its most common form, the map interrupts the North Atlantic, the South Atlantic, the South Pacific, the Indian Ocean, and the entire east/west meridian of the map.

Up to latitudes 41°44′11.8″N/S, the map is projected according to the Sinusoidal projection’s transformation. The higher latitudes are the top sections of a Mollweide projection, grafted to the Sinusoidal midsection where the scale of the two projections matches. This grafting results in a kink in the meridians along the parallel of the graft. The projection’s equal-area property follows from the fact that its source projections are themselves both equal-area.

See also

References

    This article is issued from Wikipedia - version of the 9/30/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.