Graph product

In mathematics, a graph product is a binary operation on graphs. Specifically, it is an operation that takes two graphs G₁ and G₂ and produces a graph H with the following properties:

The vertex set of H is the Cartesian product V(G₁) × V(G₂), where V(G₁) and V(G₂) are the vertex sets of G₁ and G₂, respectively.
Two vertices (u₁, u₂) and (v₁, v₂) of H are connected by an edge if and only if the vertices u₁, u₂, v₁, v₂ satisfy conditions of a certain type (see below).

The following table shows the most common graph products, with $\sim$ ; denoting “is connected by an edge to”, and $\not \sim$ denoting non-connection. The operator symbols listed here are by no means standard, especially in older papers.

Name	Condition for ( $u_{1}$ , $u_{2}$ ) ∼ ( $v_{1}$ , $v_{2}$ ).	Dimensions	Example
Cartesian product $G\square H$	( $u_{1}$ = $v_{1}$ and $u_{2}$ $\sim$ $v_{2}$ ) or ( $u_{1}$ $\sim$ $v_{1}$ and $u_{2}$ = $v_{2}$ )	$G_{V_{1},E_{1}}\square H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1}V_{2})}$
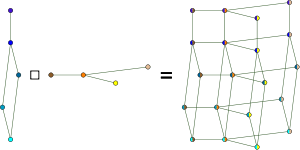Tensor product (Categorical product) $G\times H$	$u_{1}$ $\sim$ $v_{1}$ and $u_{2}$ $\sim$ $v_{2}$	$G_{V_{1},E_{1}}\times H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(2E_{1}E_{2})}$
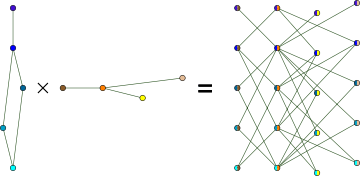Lexicographical product $G\cdot H$ or $G[H]$	u₁ ∼ v₁ or ( u₁ = v₁ and u₂ ∼ v₂ )	$G_{V_{1},E_{1}}\cdot H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1}V_{2}^{2})}$
Strong product (Normal product, AND product) $G\boxtimes H$	( u₁ = v₁ and u₂ ∼ v₂ ) or ( u₁ ∼ v₁ and u₂ = v₂ ) or ( u₁ ∼ v₁ and u₂ ∼ v₂ )	$G_{V_{1},E_{1}}\boxtimes H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(V_{1}E_{2}+V_{2}E_{1}+2E_{1}E_{2})}$
Co-normal product (disjunctive product, OR product) $G*H$	u₁ ∼ v₁ or u₂ ∼ v₂
Modular product	$(u_{1}\sim v_{1}{\text{ and }}u_{2}\sim v_{2})$ or $(u_{1}\not \sim v_{1}{\text{ and }}u_{2}\not \sim v_{2})$
Rooted product	see article	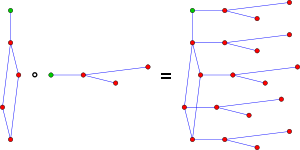$G_{V_{1},E_{1}}\cdot H_{V_{2},E_{2}}\rightarrow J_{(V_{1}V_{2}),(E_{2}V_{1}+E_{1})}$
Zig-zag product	see article	see article	see article
Replacement product
Homomorphic product^[1]^[2] $G\ltimes H$	$(u_{1}=v_{1})$ or $(u_{1}\sim v_{1}{\text{ and }}u_{2}\not \sim v_{2})$

In general, a graph product is determined by any condition for (u₁, u₂) ∼ (v₁, v₂) that can be expressed in terms of the statements u₁ ∼ v₁, u₂ ∼ v₂, u₁ = v₁, and u₂ = v₂.

Mnemonic

Let $K_{2}$ be the complete graph on two vertices (i.e. a single edge). The product graphs $K_{2}\square K_{2}$ , $K_{2}\times K_{2}$ , and $K_{2}\boxtimes K_{2}$ look exactly like the graph representing the operator. For example, $K_{2}\square K_{2}$ is a four cycle (a square) and $K_{2}\boxtimes K_{2}$ is the complete graph on four vertices. The $G[H]$ notation for lexicographic product serves as a reminder that this product is not commutative.

Notes

1 2 Roberson, David E.; Mancinska, Laura (2012). "Graph Homomorphisms for Quantum Players". arXiv:1212.1724 [quant-ph].
↑ The hom-product of ^[3] is the graph complement of the homomorphic product of.^[1]
↑ Bačík, R.; Mahajan, S. (1995). "Semidefinite programming and its applications to NP problems". Computing and Combinatorics. Lecture Notes in Computer Science. 959. p. 566. doi:10.1007/BFb0030878. ISBN 3-540-60216-X.

References

Imrich, Wilfried; Klavžar, Sandi (2000). Product Graphs: Structure and Recognition. Wiley. ISBN 0-471-37039-8{{inconsistent citations}} .

This article is issued from Wikipedia - version of the 8/15/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Graph product

Mnemonic

See also

Notes

References