H4 polytope

120-cell	600-cell

In 4-dimensional geometry, there are 15 uniform polytopes with H₄ symmetry. Two of these, the 120-cell and 600-cell, are regular.

Visualizations

Each can be visualized as symmetric orthographic projections in Coxeter planes of the H₄ Coxeter group, and other subgroups.

The 3D picture are drawn as Schlegel diagram projections, centered on the cell at pos. 3, with a consistent orientation, and the 5 cells at position 0 are shown solid.

#	Name	Coxeter plane projections						Schlegel diagrams		Net
#	Name	F4 [12]	[20]	H4 [30]	H3 [10]	A3 [4]	A2 [3]	Dodecahedron centered	Tetrahedron centered	Net
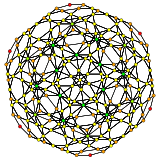
1	120-cell {5,3,3}
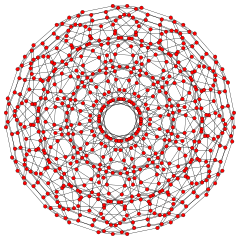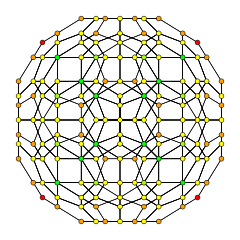
2	rectified 120-cell r{5,3,3}
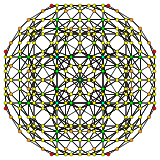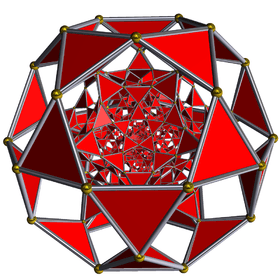3	rectified 600-cell r{3,3,5}
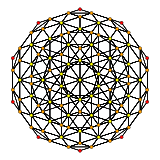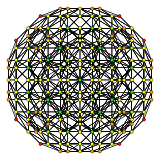4	600-cell {3,3,5}
5	truncated 120-cell t{5,3,3}
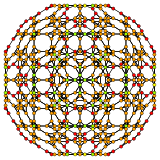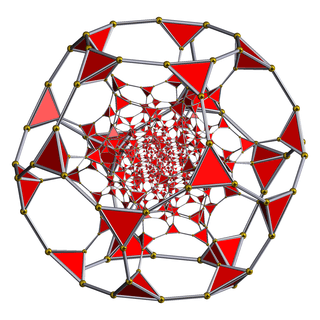6	cantellated 120-cell rr{5,3,3}
7	runcinated 120-cell (also runcinated 600-cell) t_0,3{5,3,3}
8	bitruncated 120-cell (also bitruncated 600-cell) t_1,2{5,3,3}
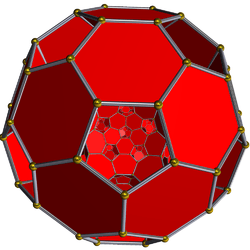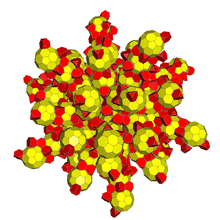9	cantellated 600-cell t_0,2{3,3,5}
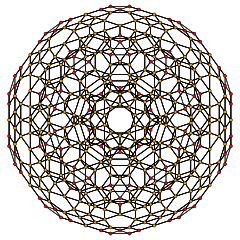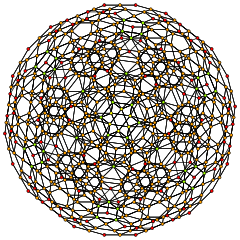10	truncated 600-cell t{3,3,5}
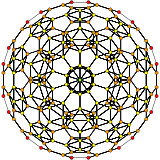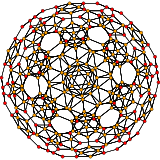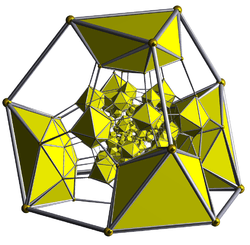11	cantitruncated 120-cell tr{5,3,3}
12	runcitruncated 120-cell t_0,1,3{5,3,3}
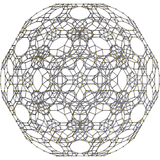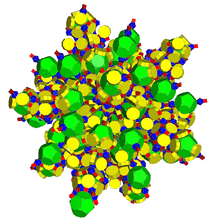13	runcitruncated 600-cell t_0,1,3{3,3,4}
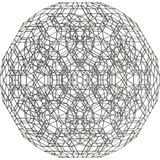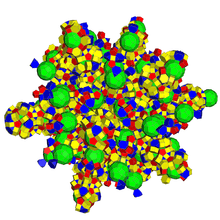14	cantitruncated 600-cell tr{3,3,5}
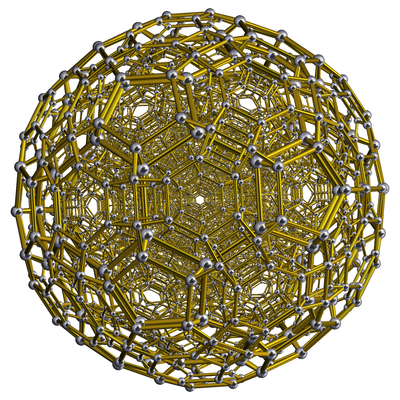15	omnitruncated 120-cell (also omnitruncated 600-cell) t_0,1,2,3{5,3,3}

Diminished forms
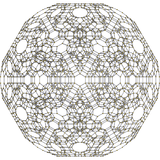#	Name	Coxeter plane projections						Schlegel diagrams		Net
#	Name	F4 [12]	[20]	H4 [30]	H3 [10]	A3 [4]	A2 [3]	Dodecahedron centered	Tetrahedron centered	Net
16	20-diminished 600-cell (grand antiprism)
17	24-diminished 600-cell (snub 24-cell)
18 Nonuniform	Bi-24-diminished 600-cell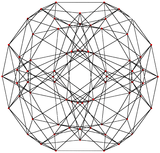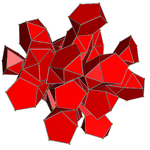
19 Nonuniform	120-diminished rectified 600-cell

Coordinates

The coordinates of uniform poyltopes from the H₄ family are complicated. The regular ones can be expressed in terms of the golden ratio φ = (1 + √5)/2 and σ = (3√5 + 1)/2. Coxeter expressed them as 5-dimensional coordinates.^[1]

n	120-cell	600-cell
4D	The 600 vertices of the 120-cell include all permutations of:^[2] (0, 0, ±2, ±2) (±1, ±1, ±1, ±√5) (±φ⁻², ±φ, ±φ, ±φ) (±φ⁻¹, ±φ⁻¹, ±φ⁻¹, ±φ²) and all even permutations of (0, ±φ⁻², ±1, ±φ²) (0, ±φ⁻¹, ±φ, ±√5) (±φ⁻¹, ±1, ±φ, ±2)	The vertices of a 600-cell centered at the origin of 4-space, with edges of length 1/φ (where φ = (1+√5) /2 is the golden ratio), can be given as follows: 16 vertices of the form:^[3] (±½, ±½, ±½, ±½), and 8 vertices obtained from (0, 0, 0, ±1) by permuting coordinates. The remaining 96 vertices are obtained by taking even permutations of ½ (±φ, ±1, ±1/φ, 0).
5D	Zero-sum permutation: (30): (√5,√5,0,-√5,-√5) (10): ±(4,-1,-1,-1,-1) (40): ±(φ⁻¹,φ⁻¹,φ⁻¹,2,-σ) (40): ±(φ,φ,φ,-2,-(σ-1)) (120): ±(φ√5,0,0,φ⁻¹√5,-√5) (120): ±(2,2,φ⁻¹√5,-φ,-3) (240): ±(φ²,2φ⁻¹,φ⁻²,-1,-2φ)	Zero-sum permutation: (20): (√5,0,0,0,-√5) (40): ±(φ²,φ⁻²,-1,-1,-1) (60): ±(2,φ⁻¹,φ⁻¹,-φ,-φ)

References

J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Wiley::Kaleidoscopes: Selected Writings of H.S.M. Coxeter
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

Notes

↑ Coxeter, Regular and Semi-Regular Polytopes II, Four-dimensional polytopes', p.296-298
↑ Weisstein, Eric W. "120-cell". MathWorld.
↑ Weisstein, Eric W. "600-cell". MathWorld.

External links

Klitzing, Richard. "4D uniform 4-polytopes".
Uniform, convex polytopes in four dimensions:, Marco Möller (German)
- 2004 Dissertation Four-dimensional Archimedean polytopes (German)
Uniform Polytopes in Four Dimensions, George Olshevsky.
- Convex uniform polychora based on the 120-cell/600-cell, George Olshevsky.
H4 uniform polytopes with coordinates: {5,3,3}, {3,3,5}, r{5,3,3},r{3,3,5}, t{3,3,5}, t{5,3,3}, rr{3,3,5}, rr{5,3,3}, tr{3,3,5}, tr{5,3,3}, 2t{5,3,3}, t03{5,3,3}, t013{3,3,5}, t013{5,3,3}, t0123{5,3,3}, grand antiprism

Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / E₉ / E₁₀ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform 4-polytope	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

This article is issued from Wikipedia - version of the 10/23/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.