Havannah

Examples of the three winning structures in Havannah, on a base-8 board. From left to right, they are the fork, the ring and the bridge.

Havannah is a two-player abstract strategy board game invented by Christian Freeling. It belongs to the family of games commonly called connection games; its relatives include Hex and TwixT. Havannah has "a sophisticated and varied strategy" and is best played on a base-10 hexagonal board, ten hex cells to a side.^[1]

The game was published for a period in Germany by Ravensburger, with a smaller, base-8 board suitable for beginners. It is nowadays only produced by Hexboards.^[2]

Game rules

One player plays as Black; the other plays as White. White starts, after which moves alternate. The rules are as follows:

• Each player places one stone of their color on the board per turn.
• Stones are never moved, captured, or otherwise changed.
• A player wins when they complete one of three different structures from unbroken lines, or paths, of connected stones, all of their colour:
  • A ring is a loop around one or more cells (no matter whether the encircled cells are occupied by any player or empty^[3]);
  • A bridge, which connects any two of the six corner cells of the board; or
  • A fork, which connects any three edges of the board; corner points are not considered parts of an edge.

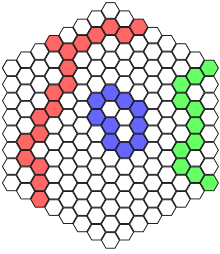
An example of all three winning combinations is shown at right. The structure in the centre of the board is a ring; the structure on the left-hand side is a fork; the structure on the right-hand side is a bridge.

Since the first player to move in Havannah has a distinct advantage, the pie rule is generally implemented for fairness. This rule allows the second player to choose whether to switch positions with the first player after the first player makes the first move.

Players of different strength can still play an interesting game when the weaker player (as White) is allowed to place two or more stones on the first turn.

Difference compared to Hex

In Hex, when the board is completely filled exactly one player will have a winning connection; in Havannah a completely filled board will have usually more than one winning structures (but the game ends with first winning structure).

Unlike in Hex, in Havannah draws are technically possible, in practice they are extremely rare. There has been one known draw between human players.^[4] Tactics are much easier to master than strategy, and differences in playing level are considerable.

Computer Havannah

In 2002 Freeling offered a prize of 1000 euros, available through 2012, for any computer program that could beat him in even one game of a ten-game match. For many years, computer programs lagged far behind human players. However, since 2010 several Havannah-playing programs have applied Monte Carlo tree search techniques resulting in some notable improvement in playing strength. The "Havannah Challenge 2012" was held October 15–19, 2012 during which Freeling played ten games against three of the strongest Havannah-playing programs available, playing (at least) one game as Black and one as White against each opponent.^[5] Freeling lost the challenge when he had to resign a game with white against the Lajkonik program.

Computational Complexity

Havannah is PSPACE-complete.^[6] The proof is by a reduction from generalized geography and is based on using ring-threats to represent the geography graph. In detail, since Lichtenstein and Sipser have proved that generalized geography remained PSPACE-hard even if the graph is only bipartite and of degree at most 3, it only remains to construct an equivalent Havannah position from such a graph, which is accomplished by constructing various gadgets in Havannah.

References

Bibliography

External links

• Official site MindSports.nl
• Havannah article on Sensei's Library
• Havannah at BoardGameGeek