Heptagonal tiling honeycomb
| Heptagonal tiling honeycomb | |
|---|---|
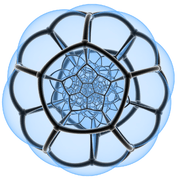
 Vertex-centered project Poincaré disk model | |
| Type | Hyperbolic regular honeycomb |
| Schläfli symbol | {7,3,3} |
| Coxeter diagram | |
| Cells | {7,3}  |
| Faces | Heptagon {7} |
| Vertex figure | tetrahedron {3,3} |
| Dual | {3,3,7} |
| Coxeter group | [7,3,3] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the heptagonal tiling honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the heptagonal tiling honeycomb is {7,3,3}, with three heptagonal tilings meeting at each edge. The vertex figure of this honeycomb is an tetrahedron, {3,3}.
Related polytopes and honeycombs
It is a part of a series of regular polytopes and honeycombs with {p,3,3} Schläfli symbol, and tetrahedral vertex figures:
| {p,3,3} polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | S3 | H3 | |||||||||
| Form | Finite | Paracompact | Noncompact | ||||||||
| Name | {3,3,3} | {4,3,3} | {5,3,3} | {6,3,3} | {7,3,3} | {8,3,3} | ... {∞,3,3} | ||||
| Image |  |
 |
 |
 |
 |
||||||
| Cells {p,3} |
 {3,3} |
 {4,3} |
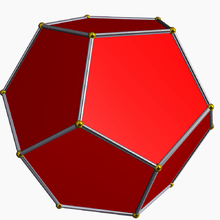 {5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
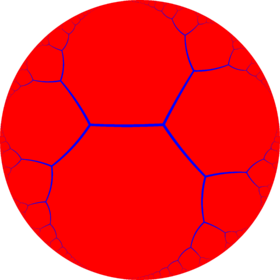 {∞,3} | ||||
See also
References
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
- Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I,II)
External links
- John Baez, Visual insights: {7,3,3} Honeycomb (2014/08/01) {7,3,3} Honeycomb Meets Plane at Infinity (2014/08/14)
- Danny Calegari, Kleinian, a tool for visualizing Kleinian groups, Geometry and the Imagination 4 March 2014.
This article is issued from Wikipedia - version of the 6/16/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.