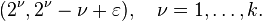Hua's lemma

In mathematics, Hua's lemma,^[1] named for Hua Loo-keng, is an estimate for exponential sums.

It states that if P is an integral-valued polynomial of degree k, $\varepsilon$ is a positive real number, and f a real function defined by

f(\alpha)=\sum_{x=1}^N\exp(2\pi iP(x)\alpha),

then

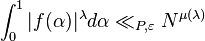\int_0^1|f(\alpha)|^\lambda d\alpha\ll_{P, \varepsilon} N^{\mu(\lambda)}

where $(\lambda,\mu(\lambda))$ lies on a polygonal line with vertices

(2^\nu,2^\nu-\nu+\varepsilon),\quad\nu=1,\ldots,k.

References

↑ Hua Loo-keng (1938). "On Waring's problem". Quarterly Journal of Mathematics 9 (1): 199–202. doi:10.1093/qmath/os-9.1.199.

This article is issued from Wikipedia - version of the 4/23/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.