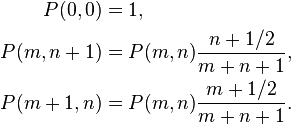Krichevsky–Trofimov estimator

In information theory, given an unknown stationary source π with alphabet A and a sample w from π, the Krichevsky–Trofimov (KT) estimator produces an estimate πi(w) of the probabilities of each symbol i ∈ A. This estimator is optimal in the sense that it minimizes the worst-case regret asymptotically.

For a binary alphabet and a string w with m zeroes and n ones, the KT estimator P(m, n) can be defined recursively:[1]

\begin{align} P(0, 0) &= 1, \\ P(m, n+1) &= P(m,n)\dfrac{n + 1/2}{m + n + 1}, \\ P(m+1, n) &= P(m,n)\dfrac{m + 1/2}{m + n + 1}. \end{align}

See also

References

  1. ↑ Krichevsky, R. E. and Trofimov V. K. (1981), "The Performance of Universal Encoding", IEEE Trans. Information Theory, Vol. IT-27, No. 2, pp. 199–207.


This article is issued from Wikipedia - version of the 5/17/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.