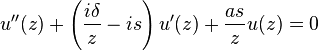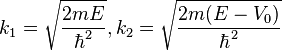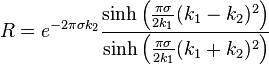Lambert-W step-potential
| Computational physics |
|---|
 |
|
Numerical analysis · Simulation |
|
Particle |
|
Scientists |
The Lambert-W step-potential[1] affords the fifth – next to those of the harmonic oscillator plus centrifugal, the Coulomb plus inverse square, the Morse, and the inverse square root[2] potentials – exact solution to the stationary one-dimensional Schrödinger equation in terms of the confluent hypergeometric functions.[3] The potential is given as
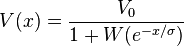 .
.
where 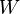 is the Lambert function also known as the product logarithm. This is an implicitly elementary function that resolves the equation
is the Lambert function also known as the product logarithm. This is an implicitly elementary function that resolves the equation 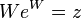 .
.
The Lambert 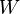 -potential is an asymmetric step of height
-potential is an asymmetric step of height 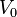 whose steepness and asymmetry are controlled by parameter
whose steepness and asymmetry are controlled by parameter  . If the space origin and the energy origin are also included, it presents a four-parametric specification of a more general five-parametric potential which is also solvable in terms of the confluent hypergeometric functions. This generalized potential, however, is a conditionally integrable one (that is, it involves a fixed parameter).
. If the space origin and the energy origin are also included, it presents a four-parametric specification of a more general five-parametric potential which is also solvable in terms of the confluent hypergeometric functions. This generalized potential, however, is a conditionally integrable one (that is, it involves a fixed parameter).
Solution
The general solution of the one-dimensional Schrödinger equation for a particle of mass 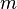 and energy
and energy 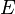 :
:
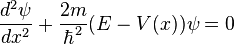 ,
,
for the Lambert 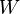 -barrier for arbitrary
-barrier for arbitrary 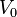 and
and  is written as
is written as
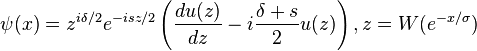 ,
,
where 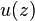 is the general solution of the scaled confluent hypergeometric equation
is the general solution of the scaled confluent hypergeometric equation
and the involved parameters are given as
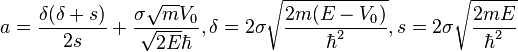 .
.
A peculiarity of the solution is that each of the two fundamental solutions composing the general solution involves a combination of two confluent hypergeometric functions.
If the quantum transmission above the Lambert 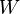 -potential is discussed, it is convenient to choose the general solution of the scaled confluent hypergeometric equation as
-potential is discussed, it is convenient to choose the general solution of the scaled confluent hypergeometric equation as
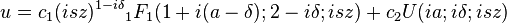 ,
,
where 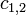 are arbitrary constants and
are arbitrary constants and 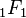 and
and 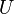 are the Kummer and Tricomi confluent hypergeometric functions, respectively. The two confluent hypergeometric functions are here chosen such that each of them stands for a separate wave moving in a certain direction. For a wave incident from the left, the reflection coefficient written in terms of the standard notations for the wave numbers
are the Kummer and Tricomi confluent hypergeometric functions, respectively. The two confluent hypergeometric functions are here chosen such that each of them stands for a separate wave moving in a certain direction. For a wave incident from the left, the reflection coefficient written in terms of the standard notations for the wave numbers
reads
See also
a/ Confluent hypergeometric potentials
- Quantum harmonic oscillator
- Hydrogen atom
- Morse potential
- Kratzer potential
- Inverse square root potential
b/ Hypergeometric potentials
- Pöschl–Teller potential
- Eckart potential
- Woods-Saxon potential
c/ Other potentials
- Rectangular potential barrier
- Finite potential well
- Infinite potential well
- Delta potential barrier (QM)
- Finite potential barrier (QM)