Monochromatic triangle

A partition of the edges of the complete graph K₅ into two triangle-free subsets

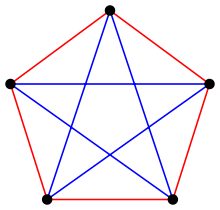
In graph theory and theoretical computer science, the monochromatic triangle problem is an algorithmic problem on graphs, in which the goal is to partition the edges of a given graph into two triangle-free subgraphs. It is NP-complete but fixed-parameter tractable on graphs of bounded treewidth.

Problem statement

The monochromatic triangle problem takes as input an n-node undirected graph G(V,E) with node set V and edge set E. The output is a Boolean value, true if the edge set E of G can be partitioned into two disjoint sets E1 and E2, such that both of the two subgraphs G1(V,E1) and G2(V,E2) are triangle-free graphs, and false otherwise. This decision problem is NP-complete.^[1]

Generalization to multiple colors

The problem may be generalized to triangle-free edge coloring, finding an assignment of colors to the edges of a graph so that no triangle has all three edges given the same color. The monochromatic triangle problem is the special case of triangle-free edge-coloring when there are exactly two colors available. If there exists a two-color triangle-free edge coloring, then the edges of each color form the two sets E1 and E2 of the monochromatic triangle problem. Conversely, if the monochromatic triangle problem has a solution, we can use one color for E1 and a second color for E2 to obtain a triangle-free edge coloring.

Connection to Ramsey's theorem

By Ramsey's theorem, for any finite number k of colors, there exists a number n such that complete graphs of n or more vertices do not have triangle-free edge colorings with k colors. For k = 2, the corresponding value of n is 6. I.e., the answer to the monochromatic triangle problem on the complete graph K₆ is no.

Parameterized complexity

It is straightforward to express the monochromatic triangle problem in the monadic second-order logic of graphs (MSO₂), by a logical formula that asserts the existence of a partition of the edges into two subsets such that there do not exist three mutually adjacent vertices whose edges all belong to the same side of the partition. It follows from Courcelle's theorem that the monochromatic triangle problem is fixed-parameter tractable on graphs of bounded treewidth. More precisely, there is an algorithm for solving the problem whose running time is the number of vertices of the input graph multiplied by a quickly-growing but computable function of the treewidth.^[2]

References