n-vector model
The n-vector model or O(n) model, introduced by H. Eugene Stanley,[1] is one of the many highly simplified models in the branch of physics known as statistical mechanics. In the n-vector model, n-component, unit length, classical spins 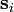 are placed on the vertices of a lattice. The Hamiltonian of the n-vector model is given by:
are placed on the vertices of a lattice. The Hamiltonian of the n-vector model is given by:
where the sum runs over all pairs of neighboring spins 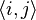 and
and  denotes the standard Euclidean inner product. Special cases of the n-vector model are:
denotes the standard Euclidean inner product. Special cases of the n-vector model are:
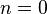 || The Self-Avoiding Walks (SAW)
|| The Self-Avoiding Walks (SAW)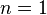 || The Ising model
|| The Ising model 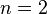 || The XY model
|| The XY model 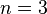 || The Heisenberg model
|| The Heisenberg model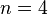 || Toy model for the Higgs sector of the Standard Model
|| Toy model for the Higgs sector of the Standard Model
The general mathematical formalism used to describe and solve the n-vector model and certain generalizations are developed in the article on the Potts model.
References
- ↑ H. E. Stanley, "Dependence of Critical Properties upon Dimensionality of Spins," Phys. Rev. Lett. 20, 589-592 (1968).
[1] H. E. Stanley, "Dependence of Critical Properties upon Dimensionality of Spins," Phys. Rev. Lett. 20, 589-592 (1968).
This paper is the basis of many articles in field theory and is reproduced as Chapter 1 of Brèzin/Wadia [eds] The Large-N expansion in Quantum Field Theory and Statistical Physics (World Scientific, Singapore, 1993). Also described extensively in the text Pathria RK Statistical Mechanics: Second Edition (Pergamon Press, Oxford, 1996).
- P.G. de Gennes, Phys. Lett. A, 38, 339 (1972) noticed that the
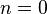 case corresponds to the SAW.
case corresponds to the SAW. - George Gaspari, Joseph Rudnick, Phys. Rev. B, 33, 3295 (1986) discuss the model in the limit of
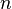 going to 0.
going to 0.