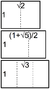
Natural logarithm of 2
The decimal value of the natural logarithm of 2 (sequence A002162 in the OEIS) is approximately
as shown in the first line of the table below. The logarithm in other bases is obtained with the formula
The common logarithm in particular is (![]() A007524)
A007524)
The inverse of this number is the binary logarithm of 10:
- (
 A020862).
A020862).
| number | approximate natural logarithm | OEIS |
|---|---|---|
| 2 | 0.693147180559945309417232121458 | A002162 |
| 3 | 1.09861228866810969139524523692 | A002391 |
| 4 | 1.38629436111989061883446424292 | A016627 |
| 5 | 1.60943791243410037460075933323 | A016628 |
| 6 | 1.79175946922805500081247735838 | A016629 |
| 7 | 1.94591014905531330510535274344 | A016630 |
| 8 | 2.07944154167983592825169636437 | A016631 |
| 9 | 2.19722457733621938279049047384 | A016632 |
| 10 | 2.30258509299404568401799145468 | A002392 |
By Lindemann–Weierstrass theorem, the natural logarithm of any natural number other than 0 and 1 (more generally, of any positive algebraic number other than 1) is a transcendental number.
Series representations
(γ is the Euler–Mascheroni constant and ζ Riemann's zeta function.)
Some Bailey–Borwein–Plouffe (BBP)-type representations fall also into this category.
Representation as integrals
(γ is the Euler–Mascheroni constant.)
Other representations
The Pierce expansion is ![]() A091846
A091846
The Engel expansion is ![]() A059180
A059180
The cotangent expansion is ![]() A081785
A081785
As an infinite sum of fractions:[1]
This generalized continued fraction:
- ,[2]
- also expressible as
Bootstrapping other logarithms
Given a value of ln(2), a scheme of computing the logarithms of other integers is to tabulate the logarithms of the prime numbers and in the next layer the logarithms of the composite numbers c based on their factorizations
Apart from the logarithms of 2, 3, 5 and 7 shown above, this employs
| prime | approximate natural logarithm | OEIS |
|---|---|---|
| 11 | 2.39789527279837054406194357797 | A016634 |
| 13 | 2.56494935746153673605348744157 | A016636 |
| 17 | 2.83321334405621608024953461787 | A016640 |
| 19 | 2.94443897916644046000902743189 | A016642 |
| 23 | 3.13549421592914969080675283181 | A016646 |
| 29 | 3.36729582998647402718327203236 | A016652 |
| 31 | 3.43398720448514624592916432454 | A016654 |
| 37 | 3.61091791264422444436809567103 | A016660 |
| 41 | 3.71357206670430780386676337304 | A016664 |
| 43 | 3.76120011569356242347284251335 | A016666 |
| 47 | 3.85014760171005858682095066977 | A016670 |
| 53 | 3.97029191355212183414446913903 | A016676 |
| 59 | 4.07753744390571945061605037372 | A016682 |
| 61 | 4.11087386417331124875138910343 | A016684 |
| 67 | 4.20469261939096605967007199636 | A016690 |
| 71 | 4.26267987704131542132945453251 | A016694 |
| 73 | 4.29045944114839112909210885744 | A016696 |
| 79 | 4.36944785246702149417294554148 | A016702 |
| 83 | 4.41884060779659792347547222329 | A016706 |
| 89 | 4.48863636973213983831781554067 | A016712 |
| 97 | 4.57471097850338282211672162170 | A016720 |
In a third layer, the logarithms of rational numbers r = a/b are computed with ln(r) = ln(a) − ln(b), and logarithms of roots via ln n√c = 1/n ln(c).
The logarithm of 2 is useful in the sense that the powers of 2 are rather densely distributed; finding powers 2i close to powers bj of other numbers b is comparatively easy, and series representations of ln(b) are found by coupling 2 to b with logarithmic conversions.
Example
If ps = qt + d with some small d, then ps/qt = 1 + d/qt and therefore
Selecting q = 2 represents ln(p) by ln(2) and a series of a parameter d/qt that one wishes to keep small for quick convergence. Taking 32 = 23 + 1, for example, generates
This is actually the third line in the following table of expansions of this type:
| s | p | t | q | d/qt |
|---|---|---|---|---|
| 1 | 3 | 1 | 2 | 1/2 = 0.50000000… |
| 1 | 3 | 2 | 2 | −1/4 = −0.25000000… |
| 2 | 3 | 3 | 2 | 1/8 = 0.12500000… |
| 5 | 3 | 8 | 2 | −13/256 = −0.05078125… |
| 12 | 3 | 19 | 2 | 7153/524288 = 0.01364326… |
| 1 | 5 | 2 | 2 | 1/4 = 0.25000000… |
| 3 | 5 | 7 | 2 | −3/128 = −0.02343750… |
| 1 | 7 | 2 | 2 | 3/4 = 0.75000000… |
| 1 | 7 | 3 | 2 | −1/8 = −0.12500000… |
| 5 | 7 | 14 | 2 | 423/16384 = 0.02581787… |
| 1 | 11 | 3 | 2 | 3/8 = 0.37500000… |
| 2 | 11 | 7 | 2 | −7/128 = −0.05468750… |
| 11 | 11 | 38 | 2 | 10433763667/274877906944 = 0.03795781… |
| 1 | 13 | 3 | 2 | 5/8 = 0.62500000… |
| 1 | 13 | 4 | 2 | −3/16 = −0.18750000… |
| 3 | 13 | 11 | 2 | 149/2048 = 0.07275391… |
| 7 | 13 | 26 | 2 | −4360347/67108864 = −0.06497423… |
| 10 | 13 | 37 | 2 | 419538377/137438953472 = 0.00305254… |
| 1 | 17 | 4 | 2 | 1/16 = 0.06250000… |
| 1 | 19 | 4 | 2 | 3/16 = 0.18750000… |
| 4 | 19 | 17 | 2 | −751/131072 = −0.00572968… |
| 1 | 23 | 4 | 2 | 7/16 = 0.43750000… |
| 1 | 23 | 5 | 2 | −9/32 = −0.28125000… |
| 2 | 23 | 9 | 2 | 17/512 = 0.03320312… |
| 1 | 29 | 4 | 2 | 13/16 = 0.81250000… |
| 1 | 29 | 5 | 2 | −3/32 = −0.09375000… |
| 7 | 29 | 34 | 2 | 70007125/17179869184 = 0.00407495… |
| 1 | 31 | 5 | 2 | −1/32 = −0.03125000… |
| 1 | 37 | 5 | 2 | 5/32 = 0.15625000… |
| 4 | 37 | 21 | 2 | −222991/2097152 = −0.10633039… |
| 5 | 37 | 26 | 2 | 2235093/67108864 = 0.03330548… |
| 1 | 41 | 5 | 2 | 9/32 = 0.28125000… |
| 2 | 41 | 11 | 2 | −367/2048 = −0.17919922… |
| 3 | 41 | 16 | 2 | 3385/65536 = 0.05165100… |
| 1 | 43 | 5 | 2 | 11/32 = 0.34375000… |
| 2 | 43 | 11 | 2 | −199/2048 = −0.09716797… |
| 5 | 43 | 27 | 2 | 12790715/134217728 = 0.09529825… |
| 7 | 43 | 38 | 2 | −3059295837/274877906944 = −0.01112965… |
Starting from the natural logarithm of q = 10 one might use these parameters:
| s | p | t | q | d/qt |
|---|---|---|---|---|
| 10 | 2 | 3 | 10 | 3/125 = 0.02400000… |
| 21 | 3 | 10 | 10 | 460353203/10000000000 = 0.04603532… |
| 3 | 5 | 2 | 10 | 1/4 = 0.25000000… |
| 10 | 5 | 7 | 10 | −3/128 = −0.02343750… |
| 6 | 7 | 5 | 10 | 17649/100000 = 0.17649000… |
| 13 | 7 | 11 | 10 | −3110989593/100000000000 = −0.03110990… |
| 1 | 11 | 1 | 10 | 1/10 = 0.10000000… |
| 1 | 13 | 1 | 10 | 3/10 = 0.30000000… |
| 8 | 13 | 9 | 10 | −184269279/1000000000 = −0.18426928… |
| 9 | 13 | 10 | 10 | 604499373/10000000000 = 0.06044994… |
| 1 | 17 | 1 | 10 | 7/10 = 0.70000000… |
| 4 | 17 | 5 | 10 | −16479/100000 = −0.16479000… |
| 9 | 17 | 11 | 10 | 18587876497/100000000000 = 0.18587876… |
| 3 | 19 | 4 | 10 | −3141/10000 = −0.31410000… |
| 4 | 19 | 5 | 10 | 30321/100000 = 0.30321000… |
| 7 | 19 | 9 | 10 | −106128261/1000000000 = −0.10612826… |
| 2 | 23 | 3 | 10 | −471/1000 = −0.47100000… |
| 3 | 23 | 4 | 10 | 2167/10000 = 0.21670000… |
| 2 | 29 | 3 | 10 | −159/1000 = −0.15900000… |
| 2 | 31 | 3 | 10 | −39/1000 = −0.03900000… |
References
- Brent, Richard P. (1976). "Fast multiple-precision evaluation of elementary functions". J. ACM. 23 (2): 242–251. doi:10.1145/321941.321944. MR 0395314.
- Uhler, Horace S. (1940). "Recalculation and extension of the modulus and of the logarithms of 2, 3, 5, 7 and 17" (PDF). Proc. Natl. Acad. Sci. U.S.A. 26: 205–212. doi:10.1073/pnas.26.3.205. MR 0001523.
- Sweeney, Dura W. (1963). "On the computation of Euler's constant". Mathematics of Computation. 17: 170–178. doi:10.1090/S0025-5718-1963-0160308-X. MR 0160308.
- Chamberland, Marc (2003). "Binary BBP-formulae for logarithms and generalized Gaussian–Mersenne primes" (PDF). Journal of Integer Sequences. 6: 03.3.7. MR 2046407.
- Gourévitch, Boris; Guillera Goyanes, Jesús (2007). "Construction of binomial sums for π and polylogarithmic constants inspired by BBP formulas" (PDF). Applied Math. E-Notes. 7: 237–246. MR 2346048.
- Wu, Qiang (2003). "On the linear independence measure of logarithms of rational numbers". Mathematics of Computation. 72 (242): 901–911. doi:10.1090/S0025-5718-02-01442-4.
- ↑ Wells, David (1997). The Penguin Dictionary of Curious and Interesting Numbers. Penguin. p. 29. ISBN 0140261494.
- ↑ Borwein, J.; Crandall, R.; Free, G. (2004). "On the Ramanujan AGM Fraction , I: The Real-Parameter Case" (PDF). Exper. Math. 13 (3): 278–280. doi:10.1080/10586458.2004.10504540.
External links
- "table of natural logarithms". PlanetMath.
- Gourdon, Xavier; Sebah, Pascal. "The logarithm constant:log 2".