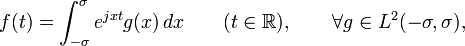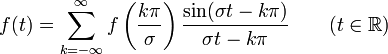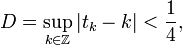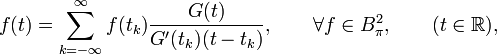Nonuniform sampling
Nonuniform sampling is a branch of sampling theory involving results related to the Nyquist–Shannon sampling theorem. Nonuniform sampling is based on Lagrange interpolation and the relationship between itself and the (uniform) sampling theorem. Nonuniform sampling is a generalisation of the Whittaker–Shannon–Kotelnikov (WSK) sampling theorem.
The sampling theory of Shannon can be generalized for the case of nonuniform samples, that is, samples not taken equally spaced in time. The Shannon sampling theory for non-uniform sampling states that a band-limited signal can be perfectly reconstructed from its samples if the average sampling rate satisfies the Nyquist condition.[1] Therefore, although uniformly spaced samples may result in easier reconstruction algorithms, it is not a necessary condition for perfect reconstruction.
The general theory for non-baseband and nonuniform samples was developed in 1967 by Henry Landau.[2] He proved that the average sampling rate (uniform or otherwise) must be twice the occupied bandwidth of the signal, assuming it is a priori known what portion of the spectrum was occupied. In the late 1990s, this work was partially extended to cover signals for which the amount of occupied bandwidth was known, but the actual occupied portion of the spectrum was unknown.[3] In the 2000s, a complete theory was developed (see the section Beyond Nyquist below) using compressed sensing. In particular, the theory, using signal processing language, is described in this 2009 paper.[4] They show, among other things, that if the frequency locations are unknown, then it is necessary to sample at least at twice the Nyquist criteria; in other words, you must pay at least a factor of 2 for not knowing the location of the spectrum. Note that minimum sampling requirements do not necessarily guarantee numerical stability.
Lagrange (polynomial) interpolation
For a given function, it is possible to construct a polynomial of degree n which has the same value with the function at n + 1 points.[5]
Let the n + 1 points to be 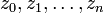 , and the n + 1 values to be
, and the n + 1 values to be 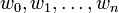 .
.
In this way, there exists a unique polynomial 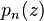 such that
such that
Furthermore, it is possible to simplify the representation of 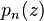 using the interpolating polynomials of Lagrange interpolation:
using the interpolating polynomials of Lagrange interpolation:
From the above equation:
As a result,
To make the polynomial form more useful:
In that way, the Lagrange Interpolation Formula appears:
Note that if 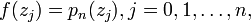 , then the above formula becomes:
, then the above formula becomes:
Whittaker–Shannon–Kotelnikov (WSK) sampling theorem
Whittaker tried to extend the Lagrange Interpolation from polynomials to entire functions. He showed that it is possible to construct the entire function[9]
which has the same value with 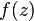 at the points
at the points 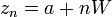
Moreover, 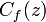 can be written in a similar form of the last equation in previous section:
can be written in a similar form of the last equation in previous section:
When a = 0 and W = 1, then the above equation becomes almost the same as WSK theorem:[10]
If a function f can be represented in the form
then f can be reconstructed from its samples as following:
Nonuniform sampling
For a sequence 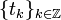 satisfying[11]
satisfying[11]
then
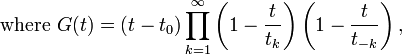 and
and 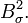 is Bernstein space
is Bernstein space
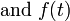 is uniformly convergent on compact sets.[12]
is uniformly convergent on compact sets.[12]
The above is called the Paley–Wiener–Levinson theorem, which generalize WSK sampling theorem from uniform samples to non uniform samples. Both of them can reconstruct a band-limited signal from those samples, respectively.
References
- ↑ Nonuniform Sampling, Theory and Practice (ed. F. Marvasti), Kluwer Academic/Plenum Publishers, New York, 2000
- ↑ H. J. Landau, “Necessary density conditions for sampling and interpolation of certain entire functions,” Acta Math., vol. 117, pp. 37–52, Feb. 1967.
- ↑ see, e.g., P. Feng, “Universal minimum-rate sampling and spectrum-blind reconstruction for multiband signals,” Ph.D. dissertation, University of Illinois at Urbana-Champaign, 1997.
- ↑ Blind Multiband Signal Reconstruction: Compressed Sensing for Analog Signals, Moshe Mishali and Yonina C. Eldar, in IEEE Trans. Signal Processing, March 2009, Vol 57 Issue 3
- ↑ Marvasti 2001, p. 124.
- ↑ Marvasti 2001, pp. 124–125.
- ↑ Marvasti 2001, p. 126.
- ↑ Marvasti 2001, p. 127.
- ↑ Marvasti 2001, p. 132.
- ↑ Marvasti 2001, p. 134.
- ↑ Marvasti 2001, p. 137.
- ↑ Marvasti 2001, p. 138.
- F. Marvasti, Nonuniform sampling: Theory and Practice. Plenum Publishers Co., 2001, pp. 123–140.
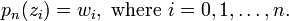
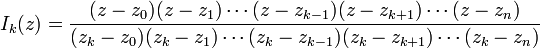
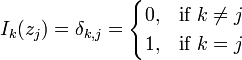
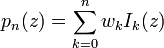
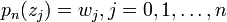
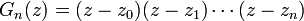
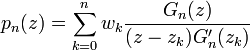
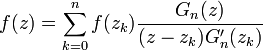
![C_f(z) = \sum_{n=-\infty}^\infty f(a+nW)\frac{\sin[\pi(z-a-nW/W)]}{[\pi(z-a-nW/W)]}](../I/m/203aaef9b226a8d92ded3849520f3568.png)
![C_f(z) = \sum_{n=-\infty}^{\infty}f(z_n)\frac{G(z)}{G'(z_n)(z-z_n)},\text{ where }G(z)=\sin[\pi(z-a)/W]\text{ and }z_n=a+nW](../I/m/ce7dd72d894e60048bcdeacd7d9d5152.png)