Pentadiagonal matrix

In linear algebra, a pentadiagonal matrix is a matrix that is nearly diagonal; to be exact, it is a matrix in which the only nonzero entries are on the main diagonal, and the first two diagonals above and below it. So it is of the form

\begin{pmatrix} c_1 & d_1 & e_1 & 0 & \cdots & \cdots & 0 \\ b_1 & c_2 & d_2 & e_2 & \ddots & & \vdots \\ a_1 & b_2 & \ddots & \ddots & \ddots & \ddots & \vdots \\ 0 & a_2 & \ddots & \ddots & \ddots & e_{n-3} & 0 \\ \vdots & \ddots & \ddots & \ddots & \ddots & d_{n-2} & e_{n-2} \\ \vdots & & \ddots & a_{n-3} & b_{n-2} & c_{n-1} & d_{n-1} \\ 0 & \cdots & \cdots & 0 & a_{n-2} & b_{n-1} & c_n \end{pmatrix}.

It follows that a pentadiagonal matrix has at most 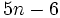5n-6 nonzero entries, where n is the size of the matrix. Hence, pentadiagonal matrices are sparse. This makes them useful in numerical analysis.

See also

This article incorporates material from Pentadiagonal matrix on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia - version of the 3/14/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.