Picture language

In formal language theory, a picture language is a set of pictures, where a picture is a 2D array of characters over some alphabet.

For example, the language 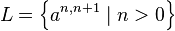$L = \left \{ a^{n,n+1} \mid n > 0 \right \}$ defines the language of squares composed of the character 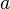$a$ . This language 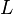$L$ contains pictures such as:

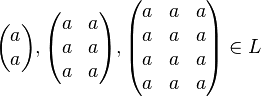
$\begin{pmatrix}a\\a\end{pmatrix}, \begin{pmatrix} a&a\\a&a\\a&a\end{pmatrix}, \begin{pmatrix} a&a&a\\a&a&a\\a&a&a\\a&a&a\end{pmatrix} \in L$

The study of picture languages was initially motivated by the problems of pattern recognition and image processing, but two-dimensional patterns also appear in the study of cellular automata and other parallel computing models. Some formal systems have been created to define picture languages, such as array grammars and tiling systems.

References

D. Giammaresi, A. Restivo. Two-dimensional languages. In A. Salomaa, G. Rozenberg (Eds.), Handbook of Formal Languages, Vol. 3, Beyond Words, Springer, Berlin, 1997, pp. 215–267.

This article is issued from Wikipedia - version of the 4/19/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.