Quotient of an abelian category

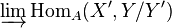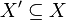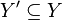In mathematics, the quotient of an abelian category A by a Serre subcategory B is the category whose objects are those of A and whose morphisms from X to Y are given by the direct limit $\varinjlim \mathrm{Hom}_A(X', Y/Y')$ over subobjects $X' \subseteq X$ and $Y' \subseteq Y$ such that 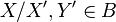$X/X', Y' \in B$ . The quotient A/B will then be an Abelian category, and there is a canonical functor 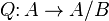$Q \colon A \to A/B$ sending an object X to itself and a morphism 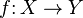$f \colon X \to Y$ to the corresponding element of the direct limit with X'=X and Y'=0. This Abelian quotient satisfies the universal property that if C is any other Abelian category, and 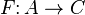$F \colon A \to C$ is an exact functor such that F(b) is a zero object of C for each 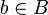$b \in B$ , then there is a unique exact functor 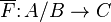$\overline{F} \colon A/B \to C$ such that 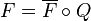$F = \overline{F} \circ Q$ .^[1]

References

↑ Gabriel, Pierre, Des categories abeliennes, Bull. Soc. Math. France 90 (1962), 323-448.

This article is issued from Wikipedia - version of the 12/24/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.