Strength of a graph

Strength of a graph: example
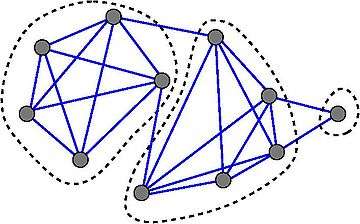
A graph with strength 2: the graph is here decomposed into three parts, with 4 edges between the parts, giving a ratio of 4/(3-1)=2.

In the branch of mathematics called graph theory, the strength of an undirected graph corresponds to the minimum ratio edges removed/components created in a decomposition of the graph in question. It is a method to compute partitions of the set of vertices and detect zones of high concentration of edges, and is analogous to graph toughness which is defined similarly for vertex removal.

Definitions

The strength $\sigma (G)$ of an undirected simple graph G = (V, E) admits the three following definitions:

Let $\Pi$ be the set of all partitions of $V$ , and $\partial \pi$ be the set of edges crossing over the sets of the partition $\pi \in \Pi$ , then $\displaystyle \sigma (G)=\min _{\pi \in \Pi }{\frac {|\partial \pi |}{|\pi |-1}}$ .
Also if ${\mathcal {T}}$ is the set of all spanning trees of G, then

\sigma (G)=\max \left\{\sum _{T\in {\mathcal {T}}}\lambda _{T}\ :\ \forall T\in {\mathcal {T}}\ \lambda _{T}\geq 0{\mbox{ and }}\forall e\in E\ \sum _{T\ni e}\lambda _{T}\leq 1\right\}.

And by linear programming duality,

\sigma (G)=\min \left\{\sum _{e\in E}y_{e}\ :\ \forall e\in E\ y_{e}\geq 0{\mbox{ and }}\forall T\in {\mathcal {T}}\ \sum _{e\in E}y_{e}\geq 1\right\}.

Complexity

Computing the strength of a graph can be done in polynomial time, and the first such algorithm was discovered by Cunningham (1985). The algorithm with best complexity for computing exactly the strength is due to Trubin (1993), uses the flow decomposition of Goldberg and Rao (1998), in time $O(\min({\sqrt {m}},n^{2/3})mn\log(n^{2}/m+2))$ .

Properties

If $\pi =\{V_{1},\dots ,V_{k}\}$ is one partition that maximizes, and for $i\in \{1,\dots ,k\}$ , $G_{i}=G/V_{i}$ is the restriction of G to the set $V_{i}$ , then $\sigma (G_{k})\geq \sigma (G)$ .
The Tutte-Nash-Williams theorem: $\lfloor \sigma (G)\rfloor$ is the maximum number of edge-disjoint spanning trees that can be contained in G.
Contrary to the graph partition problem, the partitions output by computing the strength are not necessarily balanced (i.e. of almost equal size).

References

W. H. Cunningham. Optimal attack and reinforcement of a network, J of ACM, 32:549–561, 1985.
A. Schrijver. Chapter 51. Combinatorial Optimization, Springer, 2003.
V. A. Trubin. Strength of a graph and packing of trees and branchings,, Cybernetics and Systems Analysis, 29:379–384, 1993.

This article is issued from Wikipedia - version of the 11/21/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.