Structural cohesion
Structural cohesion is the sociological conception[1][2] of a useful formal definition and measure of cohesion in social groups. It is defined as the minimal number of actors in a social network that need to be removed to disconnect the group. It is thus identical to the question of the node connectivity of a given graph. The vertex-cut version of Menger's theorem also proves that the disconnection number is equivalent to a maximally sized group with a network in which every pair of persons has at least this number of separate paths between them. It is also useful to know that k-cohesive graphs (or k-components) are always a subgraph of a k-core, although a k-core is not always k-cohesive. A k-core is simply a subgraph in which all nodes have at least k neighbors but it need not even be connected. The boundaries of structural endogamy in a kinship group are a special case of structural cohesion.
Software
Cohesive.blocking is the R program for computing structural cohesion according to the Moody-White (2003) algorithm. This wiki site provides numerous examples and a tutorial for use with R.
Examples
Some illustrative examples are presented in the gallery below:
-
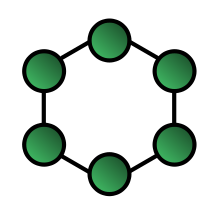
The 6-node ring in the graph has connectivity-2 or a level 2 of structural cohesion because the removal of two nodes is needed to disconnect it.
-
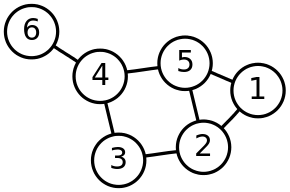
The 6-node component (1-connected) has an embedded 2-component, nodes 1-5
-
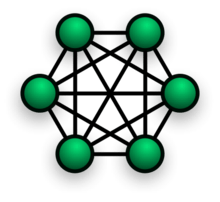
A 6-node clique is a 5-component, structural cohesion 5
Perceived cohesion
Perceived Cohesion Scale (PCS) is a six item scale that is used to measure structural cohesion in groups. In 1990, Bollen and Hoyle used the PCS and applied it to a study of large groups which were used to assess the psychometric qualities of their scale.[3]
See also
References
- ↑ N, T; White, Douglas (2003). "Structural Cohesion and Embeddedness: A Hierarchical Concept of Social Groups." (PDF). American Sociological Review. 68 (1): 1–25. doi:10.2307/3088904. Retrieved 2006-08-19.
- ↑ White, Douglas; Frank Harary (2001). "The Cohesiveness of Blocks in Social Networks: Node Connectivity and Conditional Density." (book). Sociological Methodology 2001. Blackwell Publishers, Inc., Boston, USA and Oxford, UK. 31 (1): 305–359. doi:10.1111/0081-1750.00098. Retrieved 2012-08-13.
- ↑ Chin, Wynne W., et al. Perceived Cohesion: A Conceptual and Empirical Examination: Adapting and Testing the Perceived Cohesion Scale in a Small-Group Setting. 1999. Small Group Research 30(6):751-766.