Surface diffusion

Figure 1. Model of a single adatom diffusing across a square surface lattice. Note the frequency of vibration of the adatom is greater than the jump rate to nearby sites. Also, the model displays examples of both nearest-neighbor jumps (straight) and next-nearest-neighbor jumps (diagonal). Not to scale on a spatial or temporal basis.

Surface diffusion is a general process involving the motion of adatoms, molecules, and atomic clusters (adparticles) at solid material surfaces.^[1] The process can generally be thought of in terms of particles jumping between adjacent adsorption sites on a surface, as in figure 1. Just as in bulk diffusion, this motion is typically a thermally promoted process with rates increasing with increasing temperature. Many systems display diffusion behavior that deviates from the conventional model of nearest-neighbor jumps.^[2] Tunneling diffusion is a particularly interesting example of an unconventional mechanism wherein hydrogen has been shown to diffuse on clean metal surfaces via the quantum tunneling effect.

Various analytical tools may be used to elucidate surface diffusion mechanisms and rates, the most important of which are field ion microscopy and scanning tunneling microscopy.^[3] While in principle the process can occur on a variety of materials, most experiments are performed on crystalline metal surfaces. Due to experimental constraints most studies of surface diffusion are limited to well below the melting point of the substrate, and much has yet to be discovered regarding how these processes take place at higher temperatures.^[4]

Surface diffusion rates and mechanisms are affected by a variety of factors including the strength of the surface-adparticle bond, orientation of the surface lattice, attraction and repulsion between surface species and chemical potential gradients. It is an important concept in surface phase formation, epitaxial growth, heterogeneous catalysis, and other topics in surface science.^[5] As such, the principles of surface diffusion are critical for the chemical production and semiconductor industries. Real-world applications relying heavily on these phenomena include catalytic converters, integrated circuits used in electronic devices, and silver halide salts used in photographic film.^[5]

Kinetics

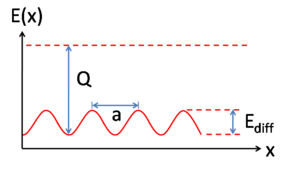
Figure 2. Diagram of the energy landscape for diffusion in one dimension. x is displacement; E(x) is energy; Q is the heat of adsorption or binding energy; a is the spacing between adjacent adsorption sites; E_diff is the barrier to diffusion.

Surface diffusion kinetics can be thought of in terms of adatoms residing at adsorption sites on a 2D lattice, moving between adjacent (nearest-neighbor) adsorption sites by a jumping process.^[1]^[6] The jump rate is characterized by an attempt frequency and a thermodynamic factor that dictates the probability of an attempt resulting in a successful jump. The attempt frequency ν is typically taken to be simply the vibrational frequency of the adatom, while the thermodynamic factor is a Boltzmann factor dependent on temperature and E_diff, the potential energy barrier to diffusion. Equation 1 describes the relationship:

\Gamma =\nu e^{{-E_{{\mathrm {diff}}}/k_{B}T}}\qquad {\text{(eq. 1)}}

Where ν and E_diff are as described above, Γ is the jump or hopping rate, T is temperature, and k_B is the Boltzmann constant. E_diff must be smaller than the energy of desorption for diffusion to occur, otherwise desorption processes would dominate. Importantly, equation 1 tells us how very strongly the jump rate varies with temperature. The manner in which diffusion takes place is dependent on the relationship between E_diff and k_BT as is given in the thermodynamic factor: when E_diff < k_BT the thermodynamic factor approaches unity and E_diff ceases to be a meaningful barrier to diffusion. This case, known as mobile diffusion, is relatively uncommon and has only been observed in a few systems.^[7] For the phenomena described throughout this article, it is assumed that E_diff >> k_BT and therefore Γ << ν. In the case of Fickian diffusion it is possible to extract both the ν and E_diff from an Arrhenius plot of the logarithm of the diffusion coefficient, D, versus 1/T. For cases where more than one diffusion mechanism is present (see below), there may be more than one E_diff such that the relative distribution between the different processes would change with temperature.

Random walk statistics describe the mean squared displacement of diffusing species in terms of the number of jumps N and the distance per jump a. The number of successful jumps is simply Γ multiplied by the time allowed for diffusion, t. In the most basic model only nearest-neighbor jumps are considered and a corresponds to the spacing between nearest-neighbor adsorption sites. The root mean squared displacement goes as $\scriptstyle {\sqrt {\langle \Delta r^{2}\rangle }}=a{\sqrt {\Gamma t}}\,\!$ (eq. 2). The diffusion coefficient is given as D = Γa²/z (eq. 3), where z = 2 for 1D diffusion as would be the case for in-channel diffusion, z = 4 for 2D diffusion, and z = 6 for 3D diffusion.^[8]

Regimes

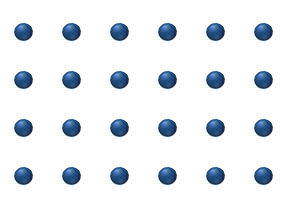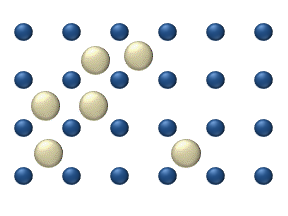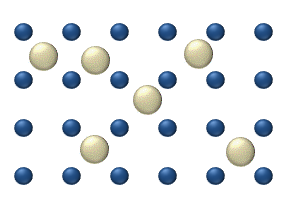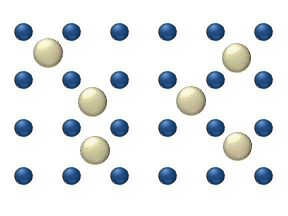
Figure 3. Model of six adatoms diffusing across a square surface lattice. The adatoms block each other from moving to adjacent sites. As per Fick’s law, flux is in the opposite direction of the concentration gradient, a purely statistical effect. The model is not intended to show repulsion or attraction, and is not to scale on a spatial or temporal basis.

There are four different general schemes in which diffusion may take place.^[9] Tracer diffusion and chemical diffusion differ in the level of adsorbate coverage at the surface, while intrinsic diffusion and mass transfer diffusion differ in the nature of the diffusion environment. Tracer diffusion and intrinsic diffusion both refer to systems where adparticles experience a relatively homogeneous environment, whereas in chemical and mass transfer diffusion adparticles are more strongly affected by their surroundings.

Tracer diffusion describes the motion of individual adparticles on a surface at relatively low coverage levels. At these low levels (< 0.01 monolayer), particle interaction is low and each particle can be considered to move independently of the others. The single atom diffusing in figure 1 is a nice example of tracer diffusion.
Chemical diffusion describes the process at higher level of coverage where the effects of attraction or repulsion between adatoms becomes important. These interactions serve to alter the mobility of adatoms. In a crude way, figure 3 serves to show how adatoms may interact at higher coverage levels. The adatoms have no "choice" but to move to the right at first, and adjacent adatoms may block adsorption sites from one another.
Intrinsic diffusion occurs on a uniform surface (e.g. lacking steps or vacancies) such as a single terrace, where no adatom traps or sources are present. This regime is often studied using field ion microscopy, wherein the terrace is a sharp sample tip on which an adparticle diffuses. Even in the case of a clean terrace the process may be influenced by non-uniformity near the edges of the terrace.
Mass transfer diffusion takes place in the case where adparticle sources and traps such as kinks, steps, and vacancies are present. Instead of being dependent only on the jump potential barrier E_diff, diffusion in this regime is now also dependent on the formation energy of mobile adparticles. The exact nature of the diffusion environment therefore plays a role in dictating the diffusion rate, since the formation energy of an adparticle is different for each type of surface feature as is described in the Terrace Ledge Kink model.

Anisotropy

Orientational anisotropy takes the form of a difference in both diffusion rates and mechanisms at the various surface orientations of a given material. For a given crystalline material each Miller Index plane may display unique diffusion phenomena. Close packed surfaces such as the fcc (111) tend to have higher diffusion rates than the correspondingly more "open" faces of the same material such as fcc (100).^[10]^[11]

Directional anisotropy refers to a difference in diffusion mechanism or rate in a particular direction on a given crystallographic plane. These differences may be a result of either anisotropy in the surface lattice (e.g. a rectangular lattice) or the presence of steps on a surface. One of the more dramatic examples of directional anisotropy is the diffusion of adatoms on channeled surfaces such as fcc (110), where diffusion along the channel is much faster than diffusion across the channel.

Mechanisms

Figure 4. Model of an atomic exchange mechanism occurring between an adatom (pink) and surface atom (silver) at a square surface lattice (blue). The surface atom becomes an adatom. Not to scale on a spatial or temporal basis.

Figure 5. Model of surface diffusion occurring via the vacancy mechanism. When surface coverage is nearly complete the vacancy mechanism dominates. Not to scale on a spatial or temporal basis.

Adatom diffusion

Diffusion of adatoms may occur by a variety of mechanisms. The manner in which they diffuse is important as it may dictate the kinetics of movement, temperature dependence, and overall mobility of surface species, among other parameters. The following is a summary of the most important of these processes:^[12]

Hopping or jumping is conceptually the most basic mechanism for diffusion of adatoms. In this model, the adatoms reside on adsorption sites on the surface lattice. Motion occurs through successive jumps to adjacent sites, the number of which depends on the nature of the surface lattice. Figures 1 and 3 both display adatoms undergoing diffusion via the hopping process. Studies have shown the presence of metastable transition states between adsorption sites wherein it may be possible for adatoms to temporarily reside.^[13]
Atomic exchange involves exchange between an adatom and an adjacent atom within the surface lattice. As shown in figure 4, after an atomic exchange event the adatom has taken the place of a surface atom and the surface atom has been displaced and has now become an adatom. This process may take place in both heterodiffusion (e.g. Pt adatoms on Ni) and self-diffusion (e.g. Pt adatoms on Pt). It is still unclear from a theoretical point of view why the atomic exchange mechanism is more predominant in some systems than in others. Current theory points towards multiple possibilities, including tensile surface stresses, surface relaxation about the adatom, and increased stability of the intermediate due to the fact that both atoms involved maintain high levels of coordination throughout the process.^[14]^[15]
Tunneling diffusion is a physical manifestation of the quantum tunneling effect involving particles tunneling across diffusion barriers. It can occur in the case of low diffusing particle mass and low E_diff, and has been observed in the case of hydrogen diffusion on tungsten and copper surfaces.^[16] The phenomenon is unique in that in the regime where the tunneling mechanism dominates, the diffusion rate is nearly temperature-independent.^[17]
Vacancy diffusion can occur as the predominant method of surface diffusion at high coverage levels approaching complete coverage. This process is akin to the manner in which pieces slide around in a "sliding puzzle". It is very difficult to directly observe vacancy diffusion due to the typically high diffusion rates and low vacancy concentration.^[18] Figure 5 shows the basic theme of this mechanism in an albeit oversimplified manner.

Figure 6. Surface diffusion jump mechanisms. Diagram of various jumps that may take place on a square lattice such as the fcc (100) plane. 1) Pink atom shown making jumps of various length to locations 2-5; 6) Green atom makes diagonal jump to location 7; 8) Grey atom makes rebound jump (atom ends up in same place it started). Non-nearest-neighbor jumps typically take place with greater frequency at higher temperatures. Not to scale.	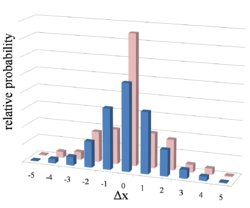Figure 7. Graph showing relative probability distribution for adatom displacement,Δx, upon diffusion in one dimension. Blue: single jumps only; Pink: double jumps occur, with ratio of single:double jumps = 1. Statistical analysis of data may yield information regarding diffusion mechanism.
Figure 8. Cross-channel diffusion involving an adatom (grey) on a channeled surface (such as fcc (110), blue plus highlighted green atom). 1) Initial configuration; 2) "Dumbbell" intermediate configuration. Final displacement may include 3, 4, 5, or even a return to the initial configuration. Not to scale.	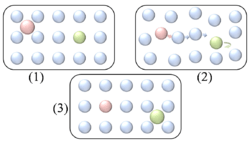Figure 9. Long range atomic exchange mechanism for surface diffusion at a square lattice. Adatom (pink), resting at surface (1), inserts into lattice disturbing neighboring atoms (2), ultimately causing one of the original substrate atoms emerge as an adatom (green) (3). Not to scale.

Recent theoretical work as well as experimental work performed since the late 1970s has brought to light a remarkable variety of surface diffusion phenomena both with regard to kinetics as well as to mechanisms. Following is a summary of some of the more notable phenomena:

Long jumps consist of adatom displacement to a non-nearest-neighbor adsorption site. They may include double, triple, and longer jumps in the same direction as a nearest-neighbor jump would travel, or they may be in entirely different directions as shown in figure 6. They have been predicted by theory to exist in many different systems, and have been shown by experiment to take place at temperatures as low as 0.1 T_m (melting temperature). In some cases data indicate long jumps dominating the diffusion process over single jumps at elevated temperatures; the phenomena of variable jump lengths is expressed in different characteristic distributions of atomic displacement over time (see figure 7).^[19]
Rebound jumps have been shown by both experiment and simulations to take place in certain systems. Since the motion does not result in a net displacement of the adatom involved, experimental evidence for rebound jumps again comes from statistical interpretation of atomic distributions. A rebound jump is shown in figure 6. The figure is slightly misleading, however, as rebound jumps have only been shown experimentally to take place in the case of 1D diffusion on a channeled surface (in particular, the bcc (211) face of tungsten).^[20]
Cross-channel diffusion can occur in the case of channeled surfaces. Typically in-channel diffusion dominates due to the lower energy barrier for diffusion of this process. In certain cases cross-channel has been shown to occur, taking place in a manner similar to that shown in figure 8. The intermediate "dumbbell" position may lead to a variety of final adatom and surface atom displacements.^[21]
Long-range atomic exchange is a process involving an adatom inserting into the surface as in the normal atomic exchange mechanism, but instead of a nearest-neighbor atom it is an atom some distance further from the initial adatom that emerges. Shown in figure 9, this process has only been observed in molecular dynamics simulations and has yet to be confirmed experimentally. In spite of this long range atomic exchange, as well as a variety of other exotic diffusion mechanisms, are anticipated to contribute substantially at temperatures currently too high for direct observation.^[22]

Figure 10. Individual mechanisms for surface diffusion of clusters. (1) Sequential displacement; (2) Edge diffusion; (3) Evaporation-condensation. In this model all three mechanisms lead to the same final cluster displacement. Not to scale.

Cluster diffusion

Cluster diffusion involves motion of atomic clusters ranging in size from dimers to islands containing hundreds of atoms. Motion of the cluster may occur via the displacement of individual atoms, sections of the cluster, or the entire cluster moving at once.^[23] All of these processes involve a change in the cluster’s center of mass.

Individual mechanisms are those that involve movement of one atom at a time.^[24]
- Edge diffusion involves movement of adatoms or vacancies at edge or kink sites. As shown in figure 10, the mobile atom maintains its proximity to the cluster throughout the process.
- Evaporation-condensation involves atoms “evaporating” from the cluster onto a terrace accompanied by “condensation” of terrace adatoms onto the cluster leading to a change in the cluster’s center of mass. While figure 10 appears to indicate the same atom evaporating from and condensing on the cluster, it may in fact be a different atom condensing from the 2D gas.
- Leapfrog diffusion is similar to edge diffusion, but where the diffusing atom actually moves atop the cluster before settling in a different location from its starting position.
- Sequential displacement refers to the process involving motion one atom at a time, moving to free nearest-neighbor sites.


(a) Dislocation	(b) Glide

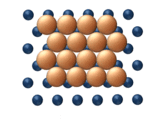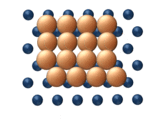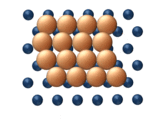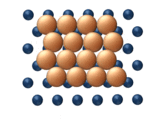(c) Reptation	(d) Shear
Figure 11. Concerted mechanisms for cluster diffusion.

Concerted mechanisms are those that involve movement of either sections of the cluster or the entire cluster all at once.^[25]
- Dislocation diffusion occurs when adjacent sub-units of a cluster move in a row-by-row fashion through displacement of a dislocation. As shown in figure 11(a) the process begins with nucleation of the dislocation followed by what is essentially sequential displacement on a concerted basis.
- Glide diffusion refers to the concerted motion of an entire cluster all at once (see figure 11(b)).
- Reptation is a snake-like movement (hence the name) involving sequential motion of cluster sub-units (see figure 11(c)).
- Shearing is a concerted displacement of a sub-unit of atoms within a cluster (see figure 11(d)).
Size-dependence: the rate of cluster diffusion has a strong dependence on the size of the cluster, with larger cluster size generally corresponding to slower diffusion. This is not, however, a universal trend and it has been shown in some systems that the diffusion rate takes on a periodic tendency wherein some larger clusters diffuse faster than those smaller than them.^[26]

Surface diffusion and heterogeneous catalysis

Surface diffusion is a critically important concept in heterogeneous catalysis, as reaction rates are often dictated by the ability of reactants to "find" each other at a catalyst surface. With increased temperature adsorbed molecules, molecular fragments, atoms, and clusters tend to have much greater mobility (see equation 1). However, with increased temperature the lifetime of adsorption decreases as the factor k_BT becomes large enough for the adsorbed species to overcome the barrier to desorption, Q (see figure 2). Reaction thermodynamics aside because of the interplay between increased rates of diffusion and decreased lifetime of adsorption, increased temperature may in some cases decrease the overall rate of the reaction.

Experimental

Surface diffusion may be studied by a variety of techniques, including both direct and indirect observations. Two experimental techniques that have proved very useful in this area of study are field ion microscopy and scanning tunneling microscopy.^[3] By visualizing the displacement of atoms or clusters over time, it is possible to extract useful information regarding the manner in which the relevant species diffuse-both mechanistic and rate-related information. In order to study surface diffusion on the atomistic scale it is unfortunately necessary to perform studies on rigorously clean surfaces and in ultra high vacuum (UHV) conditions or in the presence of small amounts of inert gas, as is the case when using He or Ne as imaging gas in field-ion microscopy experiments.

References

1 2 Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 325
↑ Antczak, Ehrlich 2007, p.39
1 2 Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 349
↑ Antczak, Ehrlich 2007, p. 50, 59
1 2 Shustorovich 1991, p. 109
↑ Shustorovich 1991, p. 109-111
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 327
↑ Structure and Dynamics of Surfaces II (Topics in Current Physics), W. Schommers, P. Von Blanckenhagen, ISBN 0387173382. Chapter 3.2, p. 75
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 330-333
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 333
↑ Shustorovich 1991, p. 114-115
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 336-340
↑ Shustorovich 1991, p. 111
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 338
↑ Antczak, Ehrlich 2007, p. 48
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 338-340
↑ Shustorovich 1991, p. 115
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 340-341
↑ Antczak, Ehrlich 2007, p. 51
↑ Antczak, Ehrlich 2007, p. 58
↑ Antczak, Ehrlich 2007, p. 40-45
↑ Antczak, Ehrlich 2007, p. 48-50
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 341
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 343-344
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 343-345
↑ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 341-343

Cited works

G. Antczak, G. Ehrlich. Surface Science Reports 62 (2007), 39-61. (Review)
Oura, K.; V.G. Lifshits; A.A. Saranin; A.V. Zotov; M. Katayama (2003). Surface Science: An Introduction. Springer-Verlag Berlin Heidelberg. ISBN 3-540-00545-5.
Shustorovich, E. (1991). Metal-Surface Reaction Energetics: Theory and Applications to Heterogeneous Catalysis, Chemisorption, and Surface Diffusion. VCH Publishers, Inc. ISBN 3-527-27938-5.

This article is issued from Wikipedia - version of the 12/3/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.