Tait equation

In fluid mechanics, the Tait equation is an equation of state, used to relate liquid density to pressure. The equation was originally published by Peter Guthrie Tait in 1888 in the form^[1]

{\frac {V_{0}-V}{(P-P_{0})V_{0}}}=-{\frac {1}{V_{0}}}{\frac {\Delta V}{\Delta P}}={\frac {A}{\Pi +(P-P_{0})}}

where $P_{0}$ is the reference pressure (taken to be 1 atmosphere), $P$ is the current pressure, $V_0$ is the volume of fresh water at the reference pressure, $V$ is the volume at the current pressure, and $A,\Pi$ are experimentally determined parameters.

Popular form of the Tait equation

Around 1895,^[1] the original isothermal Tait equation was replaced by Tammann with an equation of the form

-{\frac {1}{V}}\,{\frac {dV}{dP}}={\frac {A}{V(B+P)}}\,.

The temperature-dependent version of the above equation is popularly known as the Tait equation and is commonly written as^[2]

\beta =-{\frac {1}{V}}\left({\frac {\partial V}{\partial P}}\right)_{T}={\frac {0.4343C}{V(B+P)}}

or in the integrated form

V=V_{0}-C\log _{10}\left({\frac {B+P}{B+P_{0}}}\right)

where

$\beta$ is the compressibility of the substance (often, water) (in units of bar⁻¹ or Pa)
$V\$ is the specific volume of the substance (in units of ml/g or m³/kg)
$V_0$ is the specific volume at $P=P_{0}$ = 1 bar
$B\$ and $C\$ are functions of temperature that are independent of pressure^[2]

Pressure formula

The expression for the pressure in terms of the specific volume is

P=(B+P_{0})\,10^{\left[-{\cfrac {V-V_{0}}{C}}\right]}-B\,.

Bulk modulus formula

The tangent bulk modulus at pressure $P$ is given by

K={\frac {V(B+P)}{0.4343C}}={\cfrac {\left[V_{0}-C\log _{10}\left({\cfrac {B+P}{B+P_{0}}}\right)\right](B+P)}{0.4343C}}\,.

Murnaghan-Tait equation of state

Specific volume as a function of pressure predicted by the Tait-Murnaghan equation of state.

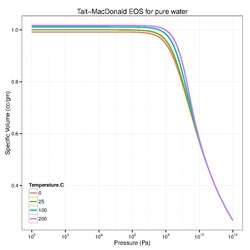
Another popular isothermal equation of state that goes by the name "Tait equation"^[3]^[4] is the Murnaghan model^[5] which is sometimes expressed as

{\frac {V}{V_{0}}}=\left[1+{\frac {n}{K_{0}}}\,(P-P_{0})\right]^{-1/n}

where $V$ is the specific volume at pressure $P$ , $V_{0}$ is the specific volume at pressure $P_{0}$ , $K_{0}$ is the bulk modulus at $P_{0}$ , and $n$ is a material parameter.

Pressure formula

This equation, in pressure form, can be written as

P={\frac {K_{0}}{n}}\left[\left({\frac {V_{0}}{V}}\right)^{n}-1\right]+P_{0}={\frac {K_{0}}{n}}\left[\left({\frac {\rho }{\rho _{0}}}\right)^{n}-1\right]+P_{0}.

where $\rho ,\rho _{0}$ are mass densities at $P,P_{0}$ , respectively. For pure water, typical parameters are $P_{0}$ = 101,325 Pa, $\rho _{0}$ = 1000 kg/cu.m, $K_{0}$ = 2.15 GPa, and $n$ = 7.15.

Note that this form of the Tate equation of state is identical to that of the Murnaghan equation of state.

Bulk modulus formula

The tangent bulk modulus predicted by the MacDonald-Tait model is

K=K_{0}\left({\frac {V_{0}}{V}}\right)^{n}\,.

Tumlirz-Tammann-Tait equation of state

Tumlirz-Tammann-Tait equation of state based on fits to experimental data on pure water.

A related equation of state that can be used to model liquids is the Tumlirz equation (sometimes called the Tammann equation and originally proposed by Tumlirz in 1909 and Tammann in 1911 for pure water).^[1]^[6] This relation has the form

V(P,S,T)=V_{\infty }-K_{1}S+{\frac {\lambda }{P_{0}+K_{2}S+P}}

where $V(P,S,T)$ is the specific volume, $P$ is the pressure, $S$ is the salinity, $T$ is the temperature, and $V_{\infty }$ is the specific volume when $P=\infty$ , and $K_{1},K_{2},P_{0}$ are parameters that can be fit to experimental data.

The Tumlirz-Tammann version of the Tait equation for fresh water, i.e., when $S=0$ , is

V=V_{\infty }+{\frac {\lambda }{P_{0}+P}}\,.

For pure water, the temperature-dependence of $V_{\infty },\lambda ,P_{0}$ are:^[6]

{\begin{aligned}\lambda &=1788.316+21.55053\,T-0.4695911\,T^{2}+3.096363\times 10^{-3}\,T^{3}-0.7341182\times 10^{-5}\,T^{4}\\P_{0}&=5918.499+58.05267\,T-1.1253317\,T^{2}+6.6123869\times 10^{-3}\,T^{3}-1.4661625\times 10^{-5}\,T^{4}\\V_{\infty }&=0.6180547-0.7435626\times 10^{-3}\,T+0.3704258\times 10^{-4}\,T^{2}-0.6315724\times 10^{-6}\,T^{3}\\&+0.9829576\times 10^{-8}\,T^{4}-0.1197269\times 10^{-9}\,T^{5}+0.1005461\times 10^{-11}\,T^{6}\\&-0.5437898\times 10^{-14}\,T^{7}+0.169946\times 10^{-16}\,T^{8}-0.2295063\times 10^{-19}\,T^{9}\end{aligned}}

In the above fits, the temperature $T$ is in degrees Celsius, $P_{0}$ is in bars, $V_{\infty }$ is in cc/gm, and $\lambda$ is in bars-cc/gm.

Pressure formula

The inverse Tumlirz-Tammann-Tait relation for the pressure as a function of specific volume is

P={\frac {\lambda }{V-V_{\infty }}}-P_{0}\,.

Bulk modulus formula

The Tumlirz-Tammann-Tait formula for the instantaneous tangent bulk modulus of pure water is a quadratic function of $P$ (for an alternative see ^[1])

K=-V\,{\frac {\partial P}{\partial V}}={\frac {V\,\lambda }{(V-V_{\infty })^{2}}}=(P_{0}+P)+{\frac {V_{\infty }}{\lambda }}(P_{0}+P)^{2}\,.

References

1 2 3 4 Hayward, A. T. J. (1967). Compressibility equations for liquids: a comparative study. British Journal of Applied Physics, 18(7), 965. http://mitran-lab.amath.unc.edu:8081/subversion/Lithotripsy/MultiphysicsFocusing/biblio/TaitEquationOfState/Hayward_CompressEqnsLiquidsComparative1967.pdf
1 2 Li, Yuan-Hui (15 May 1967). "Equation of State of Water and Sea Water" (PDF). Journal of Geophysical Research. Palisades, New York. 72 (10): 2665. Bibcode:1967JGR....72.2665L. doi:10.1029/JZ072i010p02665.
↑ Thompson, P. A., & Beavers, G. S. (1972). Compressible-fluid dynamics. Journal of Applied Mechanics, 39, 366.
↑ Kedrinskiy, V. K. (2006). Hydrodynamics of Explosion: experiments and models. Springer Science & Business Media.
↑ Macdonald, J. R. (1966). Some simple isothermal equations of state. Reviews of Modern Physics, 38(4), 669.
1 2 Fisher, F. H., and O. E. Dial Jr. Equation of state of pure water and sea water. No. MPL-U-99/67. SCRIPPS INSTITUTION OF OCEANOGRAPHY LA JOLLA CA MARINE PHYSICAL LAB, 1975. http://www.dtic.mil/dtic/tr/fulltext/u2/a017775.pdf

This article is issued from Wikipedia - version of the 11/6/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Tait equation

Popular form of the Tait equation

Pressure formula

Bulk modulus formula

Murnaghan-Tait equation of state

Pressure formula

Bulk modulus formula

Tumlirz-Tammann-Tait equation of state

Pressure formula

Bulk modulus formula

See also

References