Velocity gradient
Consider a velocity field like a fluid flowing through a pipe, here we can observe that the layer of fluid in contact with the pipe tends to be in rest with respect to the pipe. This is called no slip condition. If the velocity difference of fluid layers at the centre of the pipe and at the sides of the pipe is sufficiently small then, the fluid flow is observed in the form of continuous layers. This type of flow is called laminar flow
The flow velocity difference between adjacent layers can be measured in terms of velocity gradient. It is given by ∆u/∆y
∆u = Flow velocity difference between the layers
∆y = Distance between the layers
Relevance
The study of velocity gradients is useful in analysing path dependent materials and in the subsequent study about stresses and strains, e.g. Plastic deformation of metals. The near-wall velocity gradient of the unburned reactants flowing from a tube is a key parameter for characterizing flame stability. Stable flames exist when the velocity gradient disallows flashback into the tube, but is not so high that the flame blows-off of the end of the tube, and is thus extinguished.
Dimensional formula
We know that the dimensional formula of velocity= M0L1T−1 From the definition of velocity gradient
Velocity Gradient = velocity/distance.
Therefore Dimensional Formula of Velocity Gradient = M0L0T−1 From the above dimensional formula SI unit of Velocity Gradient is s−1
Relationship between shear stress and the velocity field
Shear stress is directly proportional to the velocity gradient as proposed by Sir Isaac Newton
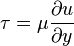 .
.
Here the constant of proportionality is called dynamic viscosity or for general use coefficient of viscosity.
See also
- Finite strain theory#Time-derivative of the deformation gradient, the spatial and material velocity gradient from continuum mechanics
References
- http://faculty.poly.edu/~rlevicky/Handout2_6333.pdf
- http://www.infoplease.com/encyclopedia/science/viscosity-the-velocity-gradient.html
- http://www.answers.com/topic/velocity-gradient
- http://www.azformula.com/physics/dimensional-formulae/what-is-dimensional-formula-of-velocity-gradient/
- https://en.wikibooks.org/wiki/Fluid_Mechanics/Fluid_Properties
- Grumer, J. , M. E. Harris, and V. R. Rowe. Fundamental Flashback, Blowoff, and Yellow-Tip Limits of Fuel Gas-Air Mixtures. Bureau of Mines, US Dept of the Interior, RI 5225, Jul 1956