Nested stack automaton
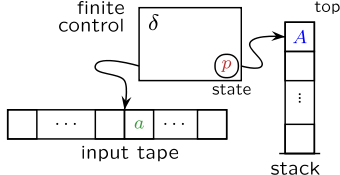
In automata theory, a nested stack automaton is a finite automaton that can make use of a stack containing data which can be additional stacks.[1] Like a stack automaton, a nested stack automaton may step up or down in the stack, and read the current symbol; in addition, it may at any place create a new stack, operate on that one, eventually destroy it, and continue operating on the old stack. This way, stacks can be nested recursively to an arbitrary depth; however, the automaton always operates on the innermost stack only.
A nested stack automaton is capable of recognizing an indexed language,[2] and in fact the class of indexed languages is exactly the class of languages accepted by one-way nondeterministic nested stack automata.[1][3]
Nested stack automata should not be confused with embedded pushdown automata, which have less computational power.
Formal definition
Automaton
A (nondeterministic two-way) nested stack automaton is a tuple ‹Q,Σ,Γ,δ,q0,Z0,F,[,],]› where
- Q, Σ, and Γ is a nonempty finite set of states, input symbols, and stack symbols, respectively,
- [, ], and ] are distinct special symbols not contained in Σ ∪ Γ,
- [ is used as left endmarker for both the input string and a (sub)stack string,
- ] is used as right endmarker for these strings,
- ] is used as the final endmarker of the string denoting the whole stack.[note 1]
- An extended input alphabet is defined by Σ' = Σ ∪ {[,]}, an extended stack alphabet by Γ' = Γ ∪ {]}, and the set of input move directions by D = {-1,0,+1}.
- δ, the finite control, is a mapping from Q × Σ' × (Γ' ∪ [Γ' ∪ {], []}) into finite subsets of Q × D × ([Γ* ∪ D), such that δ maps[note 2]
| Q × Σ' × [Γ | into subsets of Q × D × [Γ* | (pushdown mode), | |
| Q × Σ' × Γ' | into subsets of Q × D × D | (reading mode), | |
| Q × Σ' × [Γ' | into subsets of Q × D × {+1} | (reading mode), | |
| Q × Σ' × {]} | into subsets of Q × D × {-1} | (reading mode), | |
| Q × Σ' × (Γ' ∪ [Γ') | into subsets of Q × D × [Γ*] | (stack creation mode), and | |
| Q × Σ' × {[]} | into subsets of Q × D × {ε}, | (stack destruction mode), |
- Informally, the top symbol of a (sub)stack together with its preceding left endmarker "[" is viewed as a single symbol;[4] then δ reads
- the current state,
- the current input symbol, and
- the current stack symbol,
- and outputs
- the next state,
- the direction in which to move on the input, and
- the direction in which to move on the stack, or the string of symbols to replace the topmost stack symbol.
- q0 ∈ Q is the initial state,
- Z0 ∈ Γ is the initial stack symbol,
- F ⊆ Q is the set of final states.
Configuration
A configuration, or instantaneous description of such an automaton consists in a triple ‹ q, [a1a2...ai...an-1], [Z1X2...Xj...Xm-1] ›, where
- q ∈ Q is the current state,
- [a1a2...ai...an-1] is the input string; for convenience, a0 = [ and an = ] is defined[note 3] The current position in the input, viz. i with 0 ≤ i ≤ n, is marked by underlining the respective symbol.
- [Z1X2...Xj...Xm-1] is the stack, including substacks; for convenience, X1 = [Z1 [note 4] and Xm = ] is defined. The current position in the stack, viz. j with 1 ≤ j ≤ m, is marked by underlining the respective symbol.
Example
An example run (input string not shown):
| Action | Step | Stack | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1: | [a | b | [k | ] | [p | ] | c | ] | |||||
| create substack | 2: | [a | b | [k | ] | [p | [r | s | ] | ] | c | ] | |
| pop | 3: | [a | b | [k | ] | [p | [s | ] | ] | c | ] | ||
| pop | 4: | [a | b | [k | ] | [p | [] | ] | c | ] | |||
| destroy substack | 5: | [a | b | [k | ] | [p | ] | c | ] | ||||
| move down | 6: | [a | b | [k | ] | [p | ] | c | ] | ||||
| move up | 7: | [a | b | [k | ] | [p | ] | c | ] | ||||
| move up | 8: | [a | b | [k | ] | [p | ] | c | ] | ||||
| push | 9: | [a | b | [k | ] | [n | o | p | ] | c | ] | ||
Properties
When automata are allowed to re-read their input ("two-way automata"), nested stacks do not result in additional language recognition capabilities, compared to plain stacks.[5]
Gilman and Shapiro used nested stack automata to solve the word problem in certain groups.[6]
Notes
- ↑ Aho originally used "$", "¢", and "#" instead of "[", "]", and "]", respectively. See Aho (1969), p.385 top.
- ↑ Juxataposition denotes string (set) concatenation, and has a higher binding priority than set union ∪. For example, [Γ' denotes the set of all length-2 strings starting with "[" and ending with a symbol from Γ'.
- ↑ Aho originally used the left and right stack marker, viz. $ and ¢, as right and left input marker, respectively.
- ↑ The top symbol of a (sub)stack together with its preceding left endmarker "[" is viewed as a single symbol.
References
- 1 2 Aho, Alfred (1969). "Nested stack automata". Journal of the ACM. 16 (3): 383–406. doi:10.1145/321526.321529. ISSN 0004-5411.
- ↑ Partee, Barbara; Alice ter Meulen; Robert E. Wall (1990). Mathematical Methods in Linguistics. Kluwer Academic Publishers. pp. 536–542. ISBN 978-90-277-2245-4.
- ↑ John E. Hopcroft, Jeffrey D. Ullman (1979). Introduction to Automata Theory, Languages, and Computation. Addison-Wesley. ISBN 0-201-02988-X. Here:p.390
- ↑ Aho (1969), p.385 top
- ↑ C. Beeri (1975). "Two-Way Nested Stack Automata Are Equivalent to Two-Way Stack Automata" (PDF). J. Comp. and System Sciences. 10: 317–339. doi:10.1016/s0022-0000(75)80004-3.
- ↑ Robert Gilman, Michael Shapiro (Dec 1998). On Groups Whose Word Problem is Solved by a Nested Stack Automaton (PDF) (Technical report). arXiv. p. 16.
