Superstripes

Superstripes is a generic name for a phase with spatial broken symmetry that favors the onset of superconducting or superfluid quantum order. This scenario emerged in the 1990s when no-homogeneous metallic heterostructures at the atomic limit with a broken spatial symmetry have been found to favor superconductivity.[1][2] Before a broken spatial symmetry was expected to compete and suppress the superconducting order. The driving mechanism for the amplification of the superconductivity critical temperature in superstripes matter has been proposed to be the shape resonance in the energy gap parameters ∆n that is a type of Fano resonance for coexisting condensates.[3][4]

The superstripes show multigap superconductivity near a 2.5 Lifshitz transition where the renormalization of chemical potential at the metal-to-superconductor transition is not negligeable and the self-consistent solution of the gaps equation is required. The superstripes lattice scenario is made of puddles of multigap superstripes matter forming a superconducting network where different gaps are not only different in different portions of the k-space but also in different portions of the real space with a complex scale free distribution of Josephson junctions.

History

The term superstripes was introduced in 2000 at the international conference on "Stripes and High Tc Superconductivity" held in Rome to describe the particular phase of matter where a broken symmetry appearing at a transition from a phase with higher dimensionality N (3D or 2D) to a phase with lower dimensionality N-1 (2D or 1D) favors the superconducting or superfluid phase and it could increase the normal to superconducting transition temperature with the possible emergence of high-temperature superconductivity. The term superstripes scenario was introduced to make the key difference with the stripes scenario where the phase transition from a phase with higher dimensionality N (like a 2D electron gas) to the phase with broken symmetry and lower dimensionality (like a quasi 1D striped fluid) competes and suppresses the transition temperature to the superfluid phase and favors modulated striped magnetic ordering. In the broken symmetry of superstripes phase the structural modulation coexists and favors high-temperature superconductivity.[1]

High-temperature superconductivity in heterostructures at atomic limit

The prediction of high-temperature superconductivity transition temperatures is rightly considered to be one of the most difficult problems in theoretical physics. The problem remained elusive for many years since these materials have generally a very complex structure making unuseful theoretical modelling for a homogeneous system. The advances in experimental investigation on local lattice fluctuations have driven the community to the conclusion that it is a problem of quantum physics in complex matter. A growing paradigm for high-temperature superconductivity in superstripes is that a key term is the quantum interference effect between pairing channels, i.e., a resonance in the exchange-like, Josephson-like pair transfer term between different condensates. The quantum configuration interaction between different pairing channels is a particular case of shape resonance belonging to the group of Fano Feshbach resonances in atomic and nuclear physics. The critical temperature shows a suppression, due to a Fano antiresonance, when the chemical potential is tuned at a band edge where a new Fermi surface spot appears i.e., an "electronic topological transition" (ETT) or 2.5 Lifshitz transition or, a metal-to-metal topological transition. The Tc amplification is switched on when the chemical potential is tuned above the band edge in an energy region away from the band edge of the order of 1 or 2 times the energy cut off of the pairing interaction. The Tc is further amplified at the shape resonance if in this range the Fermi surface of the appearing fermi surface spot changes its dimensionality (for example the Lifshitz transition for opening a neck in a tubular Fermi surface).[5] The tuning of the chemical potential at the shape resonance can be obtained by changing: the charge density and/or the superlattice structural parameters, and/or the superlattice misfit strain and/or the disorder. Direct evidence for shape resonances in superstripes matter is provided by the anomalous variation of the isotope effect on the critical temperature by tuning the chemical potential.[6]

Materials

Crystal structure of the tetragonal (superconductive) phase of La2CuO4: top view (top-right) and CuO6 octahedron (bottom-right).[7]

It was known that the high-temperature cuprate superconductors have a complex lattice structure.[8][9][10][11][12][13][14] In 1993 it was proposed[15] that these materials belong to a particular class of materials called heterostructures at atomic limit made of a superlattice of superconducting atomic layers intercalated by a different material with the role of spacer.

All new high-temperature superconducting materials discovered in the years 2001–2013 are heterostructures at atomic limit made of the active atomic layers: honeycomb boron layer in diborides, graphene in intercalated graphite, CoO2 atomic bbc monolayers in cobaltates, FeAs atomic fluorite monolayers in pnictides, FeSe atomic fluorite monolayers in selenides.

In these materials the joint effect of (a) increasing the lattice misfit strain to a critical value, and (b) tuning the chemical potential near a Lifshitz transition in presence of electron-electron interactions induce a lattice instability with formation of the network of superconducting striped puddles in an insulating or metallic background.

This complex scenario has been called "superstripes scenario" where the 2D atomic layers show functional lattice inhomogeneities: "ripples puddles" of local lattice distortion have been observed in La2CuO4+y[16][17] in Bi222; striped puddles of ordered dopants in the spacer layers have been seen in superoxygenated La2CuO4[18] and in YBaCuO[19] The network of superconducting striped puddles has been found also in MFeAs pnictides[20] and recently in KFeSe selenides [21]

Self-organization of lattice defects can be controlled by strain engineering.[22] and photoinduced effects.[23]

Superstripes in Bose Einstein Condensates

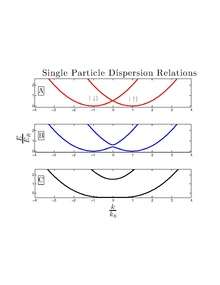
Dispersion relations of a spin orbit coupled system for different coupling strengths. Box A has no coupling. The dispersion relation shows 2 shifted free space dispersion relations. Box B shows how the gap at k=0 opens for weak coupling. Box C shows the strong coupling limit where the double degenerate minima in the first band merge into a single ground state at k=0.

Superstripes (Also called Stripe Phase) can also form in Bose Einstein Condensates (BEC) with Spin orbit coupling. The spin orbit coupling is achieved by selecting 2 spin states from the manifold of hyperfine states to couple with a two photon process.[24] For weak coupling, the resulting Hamiltonian has a spectrum with a double degenerate ground state in the first band. In this regime, the single particle dispersion relation can host a BEC in each minima.[25] The result is that the BEC has 2 momentum components which can interfere in real space. The interference pattern will appear as fringes in the density of the BEC. The periodicity of the fringes is a result of the Raman coupling beam wavelength modified by the coupling strength and by interactions within the BEC.[25] Spin orbit coupling breaks the gauge symmetry of the system and the time reversal symmetry. The formation of the stripes breaks a continuous translational symmetry.

The stripe phase is currently unobserved. Recent efforts have attempted to observe the stripe phase in a Rubidium-87 BEC, however the stripes were too small and too low contrast to be detected.[24]

References

  1. 1 2 Bianconi, A. (2000). "Superstripes". International Journal of Modern Physics B. 14 (29n31): 3289. Bibcode:2000IJMPB..14.3289B. doi:10.1142/S0217979200003769.
  2. ↑ Bianconi, A.; Di Castro, D.; Saini, N. L.; Bianconi, G. (2002). "Superstripes". Phase Transitions and Self-Organization in Electronic and Molecular Networks. Fundamental Materials Research. p. 375. doi:10.1007/0-306-47113-2_24. ISBN 978-0-306-46568-0.
  3. ↑ Perali, A.; Bianconi, A.; Lanzara, A.; Saini, N. L. (1996). "The gap amplification at a shape resonance in a superlattice of quantum stripes: A mechanism for high TC". Solid State Communications. 100 (3): 181. arXiv:1107.3292Freely accessible. Bibcode:1996SSCom.100..181P. doi:10.1016/0038-1098(96)00373-0.
  4. ↑ Bianconi, A.; Valletta, A.; Perali, A.; Saini, N. L. (1998). "Superconductivity of a striped phase at the atomic limit". Physica C: Superconductivity. 296 (3–4): 269. Bibcode:1998PhyC..296..269B. doi:10.1016/S0921-4534(97)01825-X.
  5. ↑ Innocenti, D.; Poccia, N.; Ricci, A.; Valletta, A.; Caprara, S.; Perali, A.; Bianconi, A. (2010). "Resonant and crossover phenomena in a multiband superconductor: Tuning the chemical potential near a band edge". Physical Review B. 82 (18): 184528. arXiv:1007.0510Freely accessible. Bibcode:2010PhRvB..82r4528I. doi:10.1103/physrevb.82.184528.
  6. ↑ Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. (2012). "Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensate superconductor made of a superlattice of stripes". Superconductor Science and Technology. 25 (12): 124002. arXiv:1209.1528Freely accessible. Bibcode:2012SuScT..25l4002P. doi:10.1088/0953-2048/25/12/124002.
  7. ↑ Hosono, H.; Tanabe, K.; Takayama-Muromachi, E.; Kageyama, H.; Yamanaka, S.; Kumakura, H.; Nohara, M.; Hiramatsu, H.; Fujitsu, S. (2015). "Exploration of new superconductors and functional materials, and fabrication of superconducting tapes and wires of iron pnictides". Science and Technology of Advanced Materials. 16 (3): 033503. arXiv:1505.02240Freely accessible. Bibcode:2015STAdM..16c3503H. doi:10.1088/1468-6996/16/3/033503. PMC 5099821Freely accessible. PMID 27877784.
  8. ↑ Müller, K. A. (2002). "From Phase Separation to Stripes". Stripes and Related Phenomena. Selected Topics in Superconductivity. 8. p. 1. doi:10.1007/0-306-47100-0_1. ISBN 0-306-46419-5.
  9. ↑ Müller, K. A. (2005). "Essential Heterogeneities in Hole-Doped Cuprate Superconductors". Superconductivity in Complex Systems Structure and Bonding. 114. Berlin/Heidelberg: Springer. pp. 1–11. doi:10.1007/b101015. ISBN 978-3-540-31499-8.
  10. ↑ Raveau, B. (2007). "The perovskite history: More than 60 years of research from the discovery of ferroelectricity to colossal magnetoresistance via high TC superconductivity". Progress in Solid State Chemistry. 35 (2–4): 171. doi:10.1016/j.progsolidstchem.2007.04.001.
  11. ↑ Bishop, A. R. (2008). "HTC oxides: A collusion of spin, charge and lattice". Journal of Physics: Conference Series. 108: 012027. Bibcode:2008JPhCS.108a2027B. doi:10.1088/1742-6596/108/1/012027.
  12. ↑ Bianconi, A (2000). Stripes and related phenomena. New York: Kluwer Academic/Plenum Publishers. ISBN 0-306-46419-5.
  13. ↑ Bianconi, A (2006). Symmetry and heterogeneity in high temperature superconductors. Dordrecht Great Britain: Springer. ISBN 9781402039881.
  14. ↑ Müller, K. A. (2005). Superconductivity in complex systems. Berlin New York: Springer. ISBN 978-3-540-23124-0.
  15. ↑ Bianconi, A. (1994). "On the possibility of new high Tc superconductors by producing metal heterostructures as in the cuprate perovskites". Solid State Communications. 89 (11): 933. arXiv:1107.3249Freely accessible. Bibcode:1994SSCom..89..933B. doi:10.1016/0038-1098(94)90354-9.
  16. ↑ Di Castro, D.; Colapietro, M.; Bianconi, G. (2000). "Metallic stripes in oxygen doped La2CuO4" (PDF). International Journal of Modern Physics B. 14 (29n31): 3438. Bibcode:2000IJMPB..14.3438D. doi:10.1142/S0217979200003927.
  17. ↑ Poccia, N.; Ricci, A.; Campi, G.; Fratini, M.; Puri, A.; Gioacchino, D. D.; Marcelli, A.; Reynolds, M.; Burghammer, M.; Saini, N. L.; Aeppli, G.; Bianconi, A. (2012). "Optimum inhomogeneity of local lattice distortions in La2CuO4+y". Proceedings of the National Academy of Sciences. 109 (39): 15685. arXiv:1208.0101Freely accessible. Bibcode:2012PNAS..10915685P. doi:10.1073/pnas.1208492109.
  18. ↑ Fratini, M.; Poccia, N.; Ricci, A.; Campi, G.; Burghammer, M.; Aeppli, G.; Bianconi, A. (2010). "Scale-free structural organization of oxygen interstitials in La2CuO4+y". Nature. 466 (7308): 841. arXiv:1008.2015Freely accessible. Bibcode:2010Natur.466..841F. doi:10.1038/nature09260. PMID 20703301.
  19. ↑ Campi, G.; Ricci, A.; Poccia, N.; Barba, L.; Arrighetti, G.; Burghammer, M.; Caporale, A. S.; Bianconi, A. (2013). "Scanning micro-x-ray diffraction unveils the distribution of oxygen chain nanoscale puddles in YBa2Cu3O6.33". Physical Review B. 87: 014517. arXiv:1212.2742Freely accessible. Bibcode:2013PhRvB..87a4517C. doi:10.1103/physrevb.87.014517.
  20. ↑ Caivano, R.; Fratini, M.; Poccia, N.; Ricci, A.; Puri, A.; Ren, Z. A.; Dong, X. L.; Yang, J.; Lu, W.; Zhao, Z. X.; Barba, L.; Bianconi, A. (2009). "Feshbach resonance and mesoscopic phase separation near a quantum critical point in multiband Fe As-based superconductors". Superconductor Science and Technology. 22: 014004. arXiv:0809.4865Freely accessible. Bibcode:2009SuScT..22a4004C. doi:10.1088/0953-2048/22/1/014004.
  21. ↑ Ricci, A.; Poccia, N.; Campi, G.; Joseph, B.; Arrighetti, G.; Barba, L.; Reynolds, M.; Burghammer, M.; Takeya, H.; Mizuguchi, Y.; Takano, Y.; Colapietro, M.; Saini, N. L.; Bianconi, A. (2011). "Nanoscale phase separation in the iron chalcogenide superconductor K0.8Fe1.6Se2 as seen via scanning nanofocused x-ray diffraction". Physical Review B. 84 (6): 060511. arXiv:1107.0412Freely accessible. Bibcode:2011PhRvB..84f0511R. doi:10.1103/physrevb.84.060511.
  22. ↑ Agrestini, S.; Saini, N. L.; Bianconi, G.; Bianconi, A. (2003). "The strain of CuO2 lattice: The second variable for the phase diagram of cuprate perovskites". Journal of Physics A: Mathematical and General. 36 (35): 9133. Bibcode:2003JPhA...36.9133A. doi:10.1088/0305-4470/36/35/302.
  23. ↑ Poccia, N.; Fratini, M.; Ricci, A.; Campi, G.; Barba, L.; Vittorini-Orgeas, A.; Bianconi, G.; Aeppli, G.; Bianconi, A. (2011). "Evolution and control of oxygen order in a cuprate superconductor". Nature Materials. 10 (10): 733–6. arXiv:1108.4120Freely accessible. Bibcode:2011NatMa..10..733P. doi:10.1038/nmat3088. PMID 21857676.
  24. 1 2 Galitski, Victor; Spielman, Ian B. (2013-02-07). "Spin-orbit coupling in quantum gases". Nature. 494 (7435): 49–54. arXiv:1312.3292Freely accessible. Bibcode:2013Natur.494...49G. doi:10.1038/nature11841. PMID 23389539.
  25. 1 2 Li, Yun; Pitaevskii, Lev P.; Stringari, Sandro (2012). "Quantum Tricriticality and Phase Transitions in Spin-Orbit Coupled Bose-Einstein Condensates". Physical Review Letters. 108 (22): 225301. arXiv:1202.3036Freely accessible. Bibcode:2012PhRvL.108v5301L. doi:10.1103/physrevlett.108.225301. PMID 23003610.

External links

This article is issued from Wikipedia - version of the 11/25/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.